Skydiver
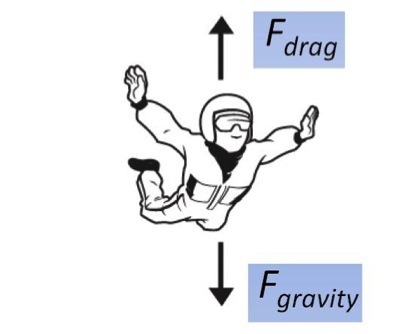 Two forces act on a parachutist. One is
the attraction by the earth, where
is the mass of the person plus equipment and
is the acceleration of gravity. The other force is the air resistance ("drag"), which is assumed to be proportional to the square of the velocity
.
Two forces act on a parachutist. One is
the attraction by the earth, where
is the mass of the person plus equipment and
is the acceleration of gravity. The other force is the air resistance ("drag"), which is assumed to be proportional to the square of the velocity
.
Using Newton's second law of motion (mass acceleration = net force applied), set up an ordinary differential equation for
Let denote the drag coefficient.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
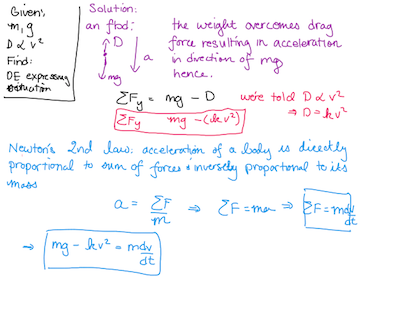
We are given the following information: m g , k and v and we are asked set up an ODE for v ( t ) using Newton's Second Law which says that F n e t = m a .
Therefore, we have to figure: 1. How to set up an equation for v ( t ) 2. Determine which forces are applied on the parachutist.
(1). We know that a in F n e t = m a is really just rate of change of velocity or d t d v so we can transform law into
F n e t = m d t d v
(2). The first paragraph explains the forces which are being applied i.e. m g (our given) and "the air resistance (drag), which is assumed to be proportional to the square of the velocity v ( t ) . Furthermore, we are told that drag is represented by k . So putting these pieces together we see that the total force on the parachutist is m g − k v 2 .
So finally we have the answer:
m g − k v 2 = m d t d v