Slice it

Consider a cylinder with a length $L$ (along the $z$ -axis), radius $R$ and the following cross section:

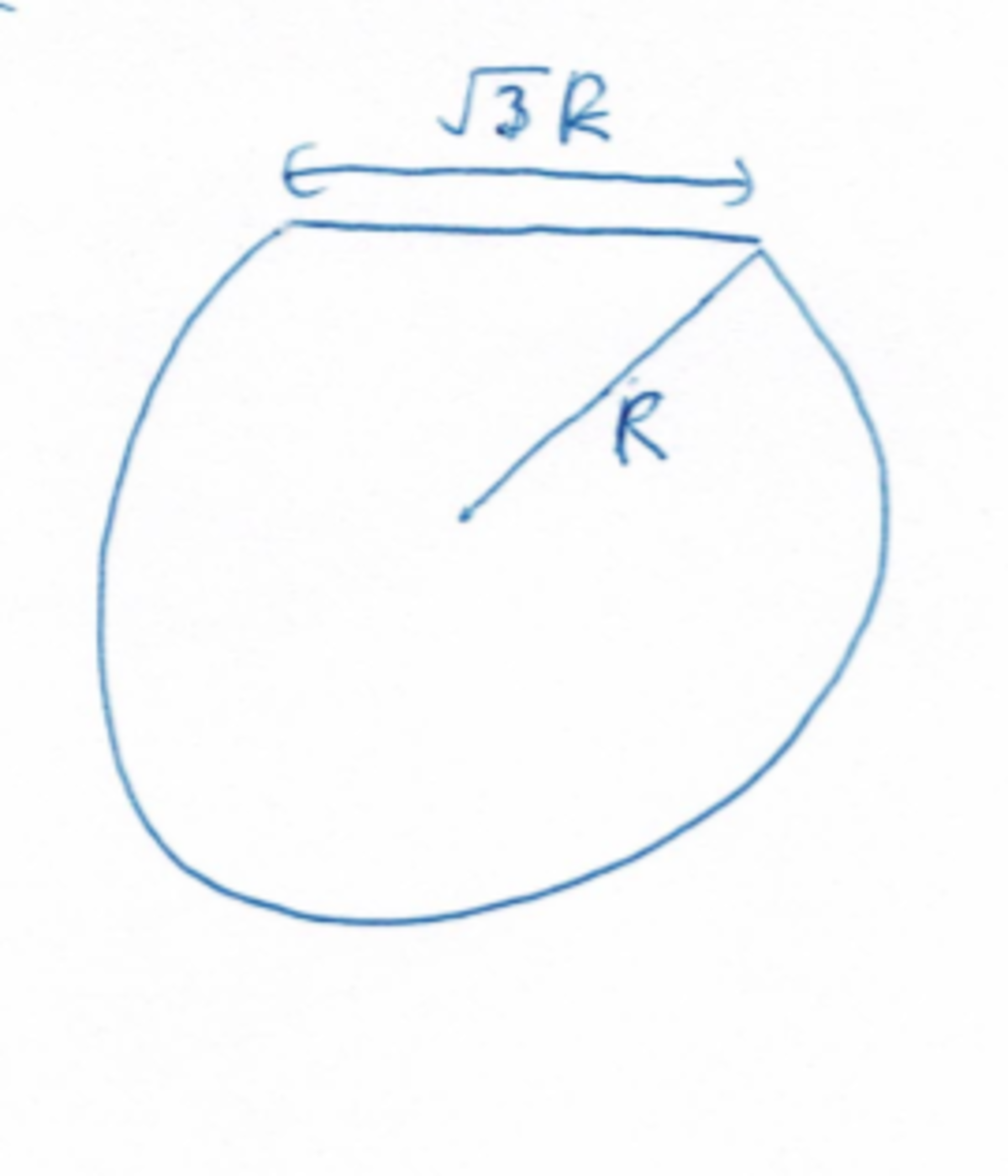
If the mass density of the cylinder is $\rho(x,y,z)=x^2+y^2$ and a segment is sliced off the top, so that the top of the cylinder in the cross section is a chord with length $\sqrt{3}R$ , then calculate the total mass of the sliced cylinder in terms of $L$ and $R$ . If this mass can be expressed as $M=LR^a(\frac{(\sqrt{b})^b+\sqrt{b}}{bc^b}-\frac{(\sqrt{b})^d+\sqrt{b}}{bc^d}+\frac{\pi}{b})$ , enter $\frac{6!}{abcd}$ .

Note: Take the origin to be at the centre of the circular cross section, with the $z$ -axis pointing along the axis of the cylinder.