Sliced Square

Geometry Level 2

A square with side lengths 3 is divided by the two lines in the diagram. Find the combined area of the blue regions.

\frac{75}{28}

\frac{81}{31}

\frac{3\sqrt{3}}{2}

Insufficient information

2 solutions

James Dirig
Dec 9, 2017

The two blue triangles are similar to each other. The area of the smaller triangle is (1/2)(3/2)(h1). The area of the larger triangle is (1/2)(2)(h2). Because the side of the square has length 3, h1 + h2 = 3.

The proportion (3/2) / h1 = 2/ h2 can be solved for h2. h2 = 4/3 h1.

Let h2 = 3 - h1. Therefore 4/3 h1 = 3 - h1. And h1 = 9/7.

The area of the smaller triangle is (1/2)(3/2)(9/7). The area of the larger triangle is (1/2)(2)(3 - 9/7).

Therefore the total area of the blue triangles is 75/28.

Another way to solve this is using integration. We can put this on a graph and specify the points, then we can get the equation of the two straight lines, y=3-x and y=3/2-7x/6. They intersect at 3-x=3/2-7x/6, simplifying we get 3/2-7x/6=0 and we can get x here which equals to 9/7. Now we have the limits of x, from 0 to 9/7 and from 9/7 to 3.

We integrate as follows:

-First integral ( x from 0 to 9/7 ) for (3/2-7x/6)dx, evaluating we get 27/28 -Second integral ( x from 9/7 to 3 ) for -(3/2-7x/6)dx , evaluating we get 12/7

Now adding both of them to get the area, 27/28+12/7=75/28

Therefore, area for the two blue regions is 75/28

Diana Al-Qassim - 3 years, 5 months ago

Mahdi Raza
Jun 13, 2020

Similarity

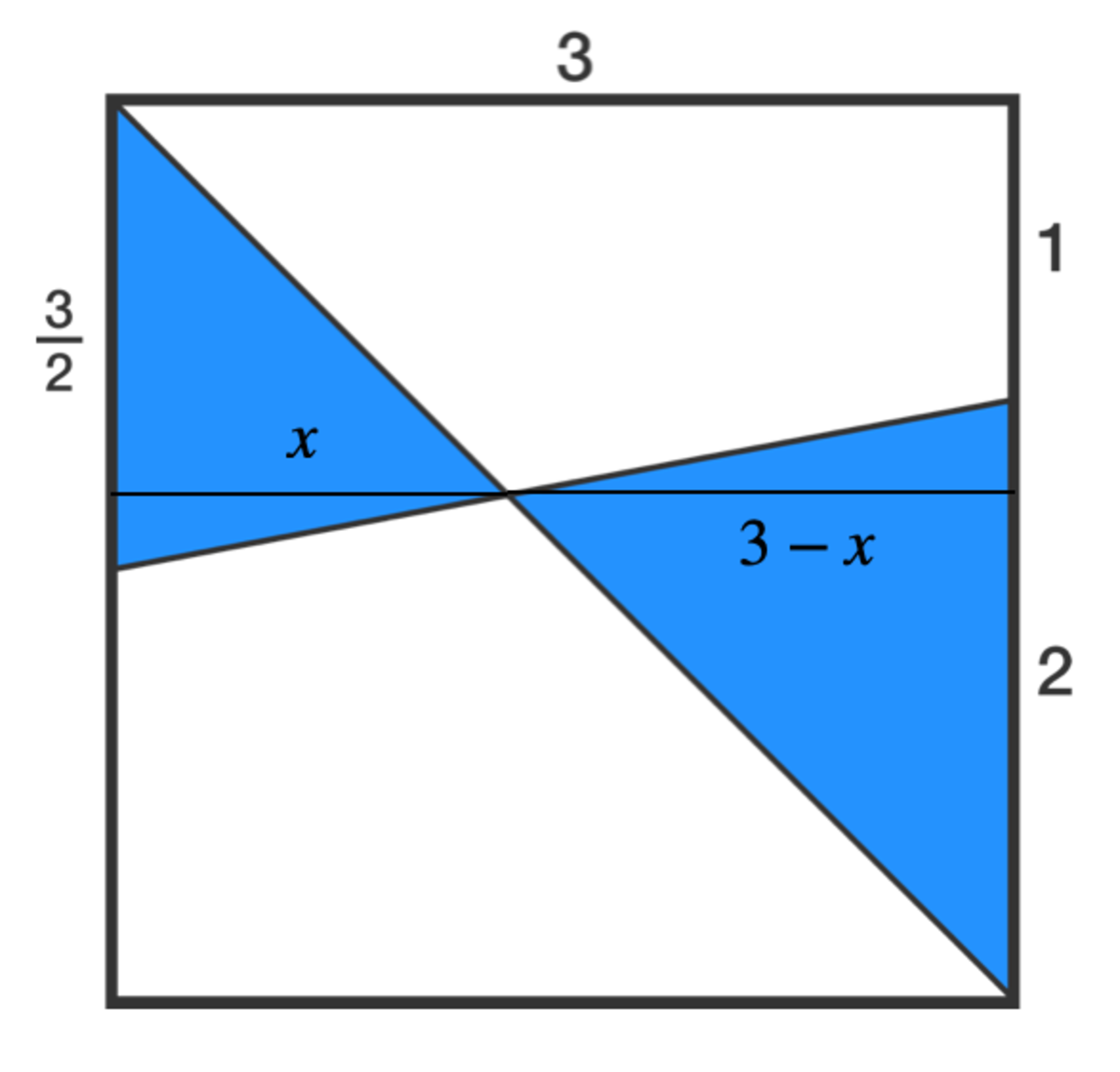
The two triangles are similar to each other, by $AA$ similarity. Thus

$\dfrac{x}{1.5} = \dfrac{3-x}{2} \quad \implies \quad 2x + 1.5x = 4.5 \quad \implies \quad x = \dfrac{9}{7}$

Areas

$\begin{aligned} \text{Area } &= \dfrac{1}{2} (1.5x) + \dfrac{1}{2} \left (2 (3-x) \right) \\ \\ &= \dfrac{1}{2} \left(6 - \dfrac{x}{2}\right) \\ \\ &= \dfrac{1}{2} \left(\dfrac{84}{14} - \dfrac{9}{7} \cdot \dfrac{1}{2}\right) \\ \\ &= \boxed{\dfrac{75}{28}} \end{aligned}$

Sliced Square

2 solutions

Similarity

Areas

0 pending reports