Sliced square inspired
A unit square ABCD is divided as follows where AE=BE while DI is double of CI. If the total areas of triangles AEL and CLI can be expressed as b a where a and b are coprime positive integers, a + b = ?
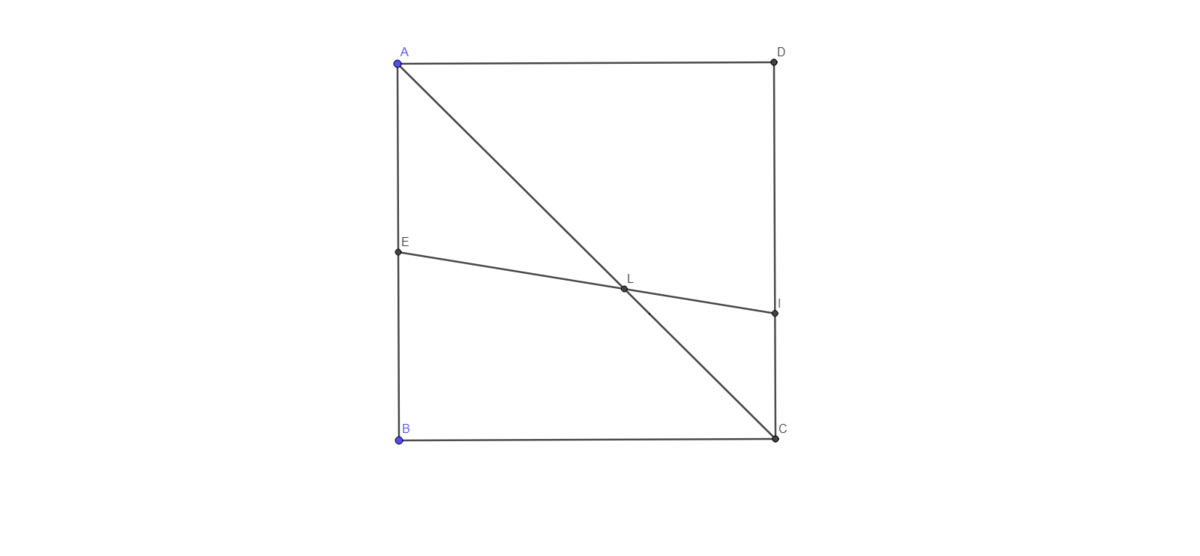
The answer is 73.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Consdering that AE=BE, A E = 2 1 and considering that DI is double of CI, D I = 2 C I so:
D I + C I = 1
( 2 + 1 ) C I = 1
3 C I = 1
C I = 3 1
Now let the perpendicular distance from L to AB be h . Then the perpendicular distance from L to CD is ( 1 − h ) . Note that AEL and CLI are similar triangles which means that:
C I A E = 1 − h h
3 1 2 1 = 1 − h h
2 3 = 1 − h h
3 − 3 h = 2 h
( 2 + 3 ) h = 3
5 h = 3
h = 5 3
Now the total area is 2 1 × ( 2 1 5 3 + 3 1 5 2 ) = 2 1 × ( 1 0 3 + 1 5 2 ) = 2 1 × 3 0 9 + 4 = 2 1 × 3 0 1 3 = 6 0 1 3 .
With a = 1 3 and b = 6 0 , a + b = 7 3 .
Rotate the square 9 0 ∘ counterclockwise and place A at the origin as shown below.
A C lies along y = x and E I lies along y = 6 x − 3 ; their intersection point L has coordinates ( 5 3 , 5 3 ) .
Then, using A E and C I as their respective bases, △ A E I has area 2 1 ( 2 1 ) ( 5 3 ) = 2 0 3 and △ C I L has area 2 1 ( 3 1 ) ( 5 2 ) = 3 0 2 .
Thus the combined area is 2 0 3 + 3 0 2 = 6 0 1 3 , so our answer is 1 3 + 6 0 = 7 3