Slicing A Dodecahedron
Geometry
Level
3
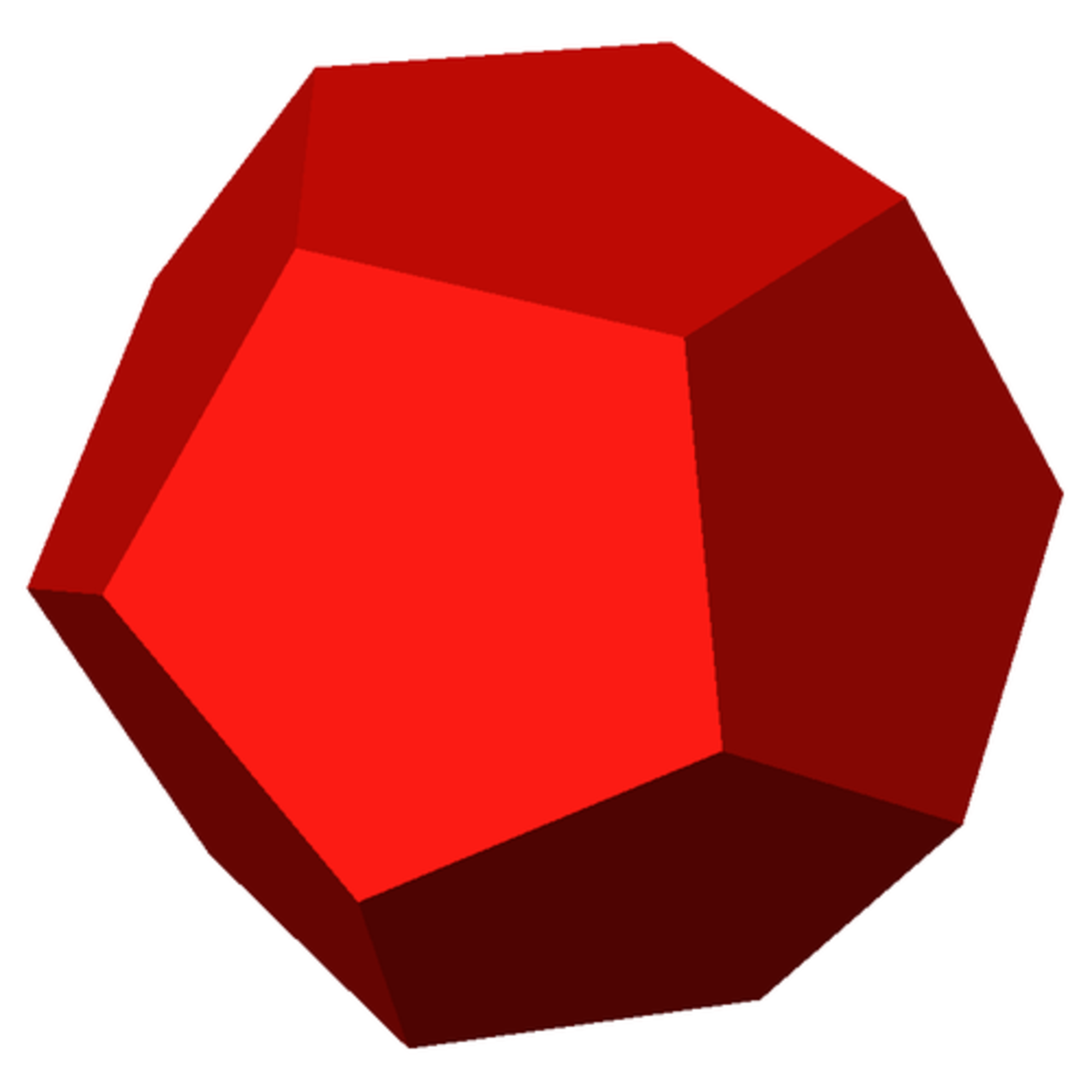
A dodecahedron is carefully balanced on one of its vertices and then sliced horizontally through its center (half way between opposite vertices). How many sides does the resulting cross-sectional area have?
Try more questions on Platonic Solids .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
When an dodecahedron is "standing" on one of its vertices, its 12 faces are oriented with 3 on the top (joined at the top vertex), 3 on the bottom (joined at the bottom vertex), and 6 around the side. These 6 around the side form the 6 sides of a hexagon.