Slicing the Diagonal
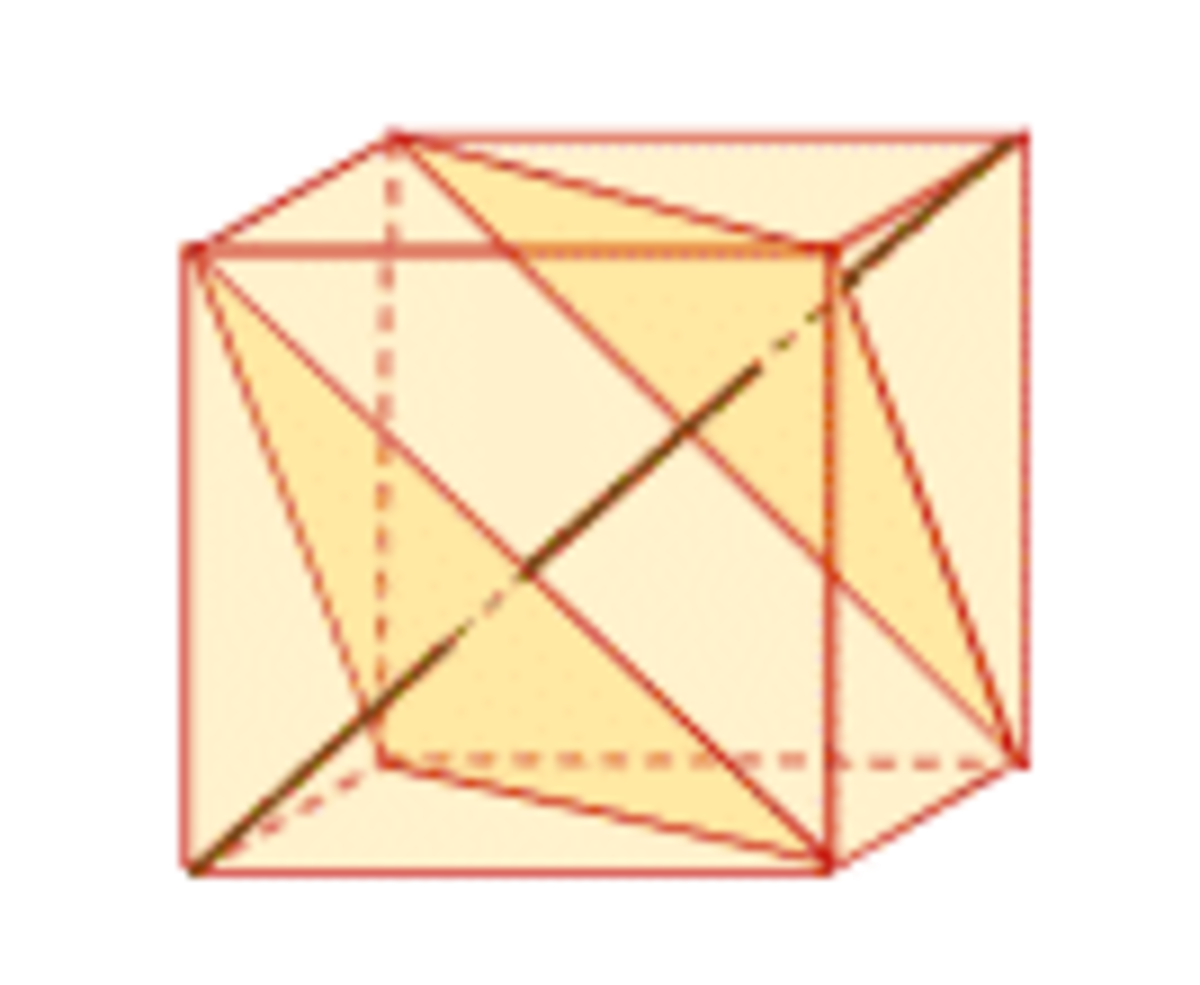 A space diagonal of a cube is sliced into three segments by two planes, each of which is perpendicular to the diagonal and goes through three of the vertices of the cube. If the lengths of the resulting segments of the diagonal are in the proportion
, report the fraction
.
A space diagonal of a cube is sliced into three segments by two planes, each of which is perpendicular to the diagonal and goes through three of the vertices of the cube. If the lengths of the resulting segments of the diagonal are in the proportion
, report the fraction
.
The answer is 1.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The D F portion of both diagonals does coincide, since F must be on line A C and D on line E G .
Since H D = D F = F B , the diagonal is divided in proportions 1 : 1 : 1 and the answer is 1 .
...
It is interesting that in 3 dimensions we have a diagonal length ( 3 ) divided into 3 sections each length 3 1 .
In 2 dimensions we have a diagonal length ( 2 ) divided into 2 sections each length 2 1 .
To stretch a point, we could say that in 1 dimension we have a segment length ( 1 ) divided into 1 section length 1 1 .
More interestingly, we could ask about 4 dimensions. The space diagonal is ( 4 ) = 2 long. Is it also divided into four equal sections each 2 1 long?