Slick Projectiles
Two projectiles are thrown horizontaly, from the same place but with different velocities v 1 , v 2 and to opposite directions. What is the separation (in meters) between the projectiles at the moment when their velocities are perpendicular one with respect to the other?
Numrical values: v 1 = 1 m/s ; v 2 = 4 m/s ; g = 1 0 m/s 2 .
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
there is very short method to solve this question in one line.. !!!!
Below is a diagram on how it would look like when the velocities are perpendicular
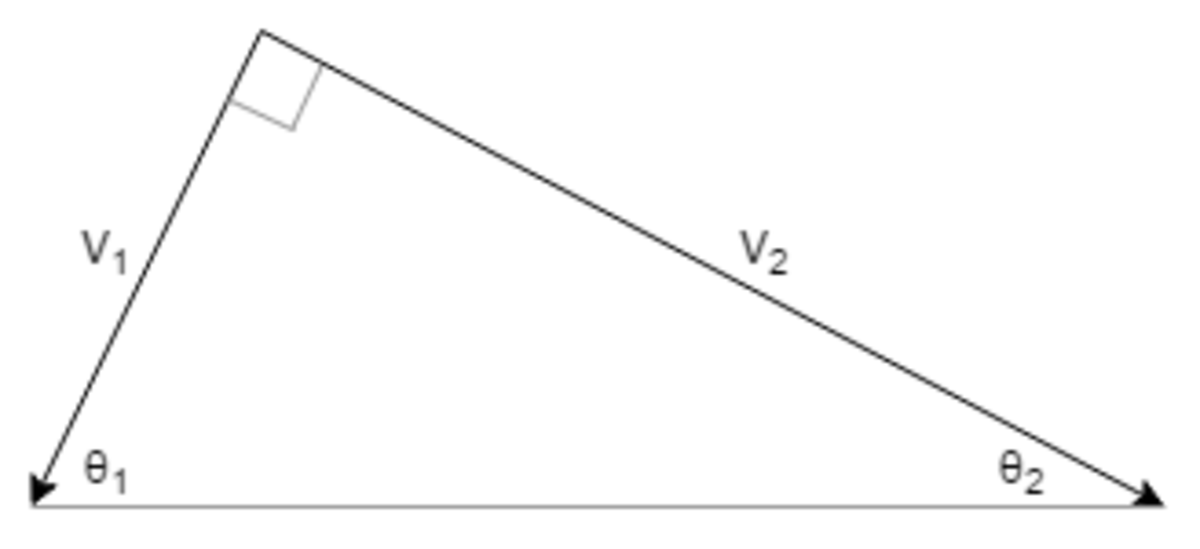 where
θ
1
=
t
a
n
−
1
(
1
g
t
) and
θ
2
=
t
a
n
−
1
(
4
g
t
).
Since we know that
θ
1
+
θ
2
=
9
0
o
, we can solve for
t
which gives
t
=
0
.
2
s
. Horizontal separation
=
(
4
+
1
)
t
=
1
m
.
where
θ
1
=
t
a
n
−
1
(
1
g
t
) and
θ
2
=
t
a
n
−
1
(
4
g
t
).
Since we know that
θ
1
+
θ
2
=
9
0
o
, we can solve for
t
which gives
t
=
0
.
2
s
. Horizontal separation
=
(
4
+
1
)
t
=
1
m
.
The slick solution is based on the fact that the point product of the velocity vectors of projectiles is zero when they are penpendicular one to the other:
V 1 • V 2 = − v 1 v 2 + 2 g h = 0 → h = 2 g v 1 v 2
The first term on the right side of the first equation is negative because the horzontal componenent of the velocities are antiparallel, both projectiles fell the same lenght, thus, they have the same velocity's vertical component. The rest are simple kinematics.
The relative movement of a projectile with respecto to the other is:
x r = ( v 1 + v 2 ) t ; y r = 0 ("r" stands for relative)
The projectiles' vertical position depend on time by:
y = 2 g t 2 → t = g 2 y
So:
x r = ( v 1 + v 2 ) g 2 y
For y=h (when they are perpendicular):
x r = ( v 1 + v 2 ) g v 1 v 2 = 1 m
The "1m" is obtained after replacing values.