Slide away

Electricity and Magnetism Level 3

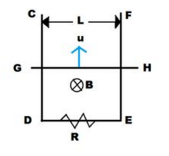
C D E F CDEF is a fixed conducting smooth frame in vertical plane. A conducting uniform rod G H GH of mass m m can move vertically and smoothly without loosing contact with the frame. G H GH always remains horizontal and is given a velocity U U upward and released. Taking acceleration due to gravity as g g and resistance attached to D E DE as R R , the time taken by the rod to reach the highest point is ___________ \text{\_\_\_\_\_\_\_\_\_\_\_} .

m R B 2 L 2 ln ⁡ ( m g R + B 2 L 2 U m g R ) \frac{mR}{{B}^{2}L^{ 2 } } \ln { \left(\frac { mgR+{ B }^{ 2 }{ L }^{ 2 }U }{ mgR } \right)} m U R B 2 L 2 ln ⁡ ( m g R + m B 2 L 2 U m g R ) \frac{mUR}{{B}^{2}L^{ 2 } } \ln { \left(\frac { mgR+{ mB }^{ 2 }{ L }^{ 2 }U }{ mgR } \right)} None of these m R B 2 L 2 ln ⁡ ( 2 m g R + 5 m B 2 L 2 U m g R ) \frac{mR}{{B}^{2}L^{2} } \ln { \left(\frac { 2mgR+5{ mB }^{ 2 }{ L }^{ 2 }U }{ mgR } \right)}

Jaswinder Singh by Jaswinder Singh , 23, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Jaswinder Singh
Mar 22, 2016

the emf induced due to motion of conductor ϵ = ∫ ( v → × B → ) . d l → \epsilon =\int { (\overrightarrow { v } \times \overrightarrow { B } ).\overrightarrow { dl } } Let the velocity of conductor at any time be "v" ϵ = B L v \epsilon =BLv Current flowing I = B L v R I=\frac { BLv }{ R } Force on the conductor F → = ∫ I d l → × B → \overrightarrow { F } =\int { \overrightarrow { Idl } \times \overrightarrow { B } } F = I L B = B 2 L 2 v R ↓ F=ILB=\frac { { B }^{ 2 }{ L }^{ 2 }v }{ R } \downarrow e q u a t i o n equation − m d v d t = B 2 L 2 v R + m g -m\frac { dv }{ dt } =\frac { { B }^{ 2 }{ L }^{ 2 }v }{ R } +mg − m d v B 2 L 2 v R + m g = d t -m\frac { dv }{ \frac { { B }^{ 2 }{ L }^{ 2 }v }{ R } +mg } =dt Integrate and solve

3 Helpful 0 Interesting 0 Brilliant 0 Confused

I did it the same way, but I think you can improve the options, by making them more tricky, because dimensional analysis ruins the problem. Only the second and third options have the dimension of time, and among them the term inside ln() which should be dimensionless is satisfied only by second option.

Of course, none of these could have been the answer, but someone mat get lucky, because now they have 2 options to choose from, the second and the fourth one.

Soumava Pal - 5 years, 2 months ago

Log in to reply

well ,to be honest i solved it using Dimensional Analysis !!! @Soumava Pal

shivam mishra - 5 years, 1 month ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...