Slide it Away
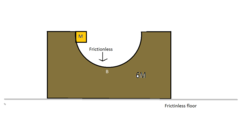A small block of mass M is kept initially as shown in figure . Find the velocity of the bigger ramp( 6M ) when the smaller block reaches the bottom most point B. take the radius of the semi circular formation of the bigger block as "R"
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
When the small block reaches down then considering block and ramp as my system we notice that there is no external force for my system in the horizontal direction ( although gravity which is an external force acts vertically) so if you apply law of conservationof momentum for horizontal direction Or the centre of mass condition M u=6M v And MgR=1/2(M u u+6M v v) Equate and solve
When the small block reaches down then considering block and ramp as my system we notice that there is no external force for my system in the horizontal direction ( although gravity which is an external force acts vertically) so if you apply law of conservationof momentum for horizontal direction Or the centre of mass condition Mu=6Mv And MgR=1/2(Muu+6Mvv) Equate and solve
First a fall observe that,out of 8 given option,there are only 2 options which are dimensionally correct ...
Now, 2 opitions remaining,i gone for 50-50 to try my luck and got the correct answer .
Cheers!!