Slide that angle!

If we draw the circumcircle of $\triangle BPC$ (centered at $O$ ), then $2\angle BPC=\angle BOC$ .

If the circumradius( $R$ ) gets smaller, then $\angle BOC$ will be bigger. So, we want the circumcircle to be tangent to $\overline{AP}$ .

Let $\overline{OH}\perp\overline{BC}$ . So, ${CH}=1$ .

${OA}^2={AH}^2+{OH}^2={OA}^2+{OC}^2-{CH}^2=9+R^2-1=8+R^2$

${AP}^2={OA}^2-{OP}^2=8+R^2-R^2=8,{AP}=2\sqrt{2}$

Notice that we doesn't really need $\angle PAB=60^\circ$

How about a solution with no trigonometry? $\angle BPC$ is maximized when the circumcircle of $\triangle BPC$ is smallest. So we just need to find the perpendicular bisectors of $\overline{PC}$ and $\overline{CB}$ .

Place $C=(0,0)$ , $A=(-2,0)$ , $B=(2,0)$ , and $P$ on the line $y=\sqrt{3}(x-2)$

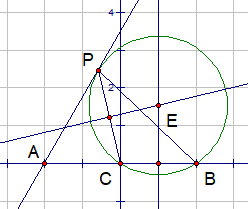
The perpendicular bisectors intersect at $E$ , we need to minimize the y-coordinate of this point.

The perpendicular bisector of $\overline{CB}$ is $x=1$

The other will take more work but is ultimately $y=\sqrt{3}\left(\frac{ax}{3a+6}+\frac{a^{2}}{6a+12}+\frac{a+2}{2}\right)$

The y-coordinate of the intersection is $\sqrt{3}\left(\frac{2a^{2}+5a+6}{3a+6}\right)$

We can minimize with a calculus derivative to find $a=\sqrt{2}-2$

This is the x-coordinate of $P$ . The horizontal distance to $A$ is $\sqrt{2}$

Finally $AP=\boxed{2\sqrt{2}}$

By law of cosines on $\triangle CAP$ , $CP^2 = AP^2 + 2^2 - 2 \cdot AP \cdot 2 \cdot \cos 60°$ , or $CP^2 = AP^2 - 2AP + 4$ .

By law of cosines on $\triangle BAP$ , $BP^2 = AP^2 + 4^2 - 2 \cdot AP \cdot 4 \cdot \cos 60°$ , or $BP^2 = AP^2 - 4AP + 16$ .

By law of cosines on $\triangle BPC$ , $2^2 = CP^2 + BP^2 - 2 \cdot CP \cdot BP \cdot \cos \angle BPC$ . Substituting the above $CP$ and $BP$ equations and rearranging, we have $\cos \angle BPC = \frac{AP^2 - 3AP + 8}{\sqrt{(AP^2 - 2AP + 4)(AP^2 - 4AP + 16)}}$ .

Using derivatives we find that $\angle BPC$ is maximized when $AP = 2\sqrt{2} \approx \boxed{2.82843}$ .

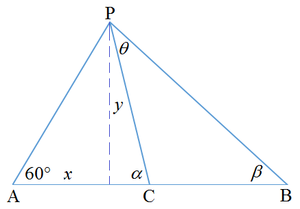
Let $A$ be the origin $(0,0)$ , then $B(4,0)$ and $C(2,0)$ . Let $P(x,y)$ , $\angle BPC = \theta$ , $\angle PCA = \alpha$ , and $\angle PBA = \beta$ . We note that $\angle BPC = \theta$ is larger when $\tan \theta$ is larger for $0^\circ \le \theta < 90^\circ$ and that

$\begin{aligned} \tan \theta & = \tan (\alpha - \beta) = \frac {\tan \alpha - \tan \beta}{1+\tan \alpha \tan \beta} \\ & = \frac {\frac y{2-x}-\frac y{4-x}}{1+\frac {y^2}{(2-x)(4-x)}} = \frac {2y}{x^2-6x+8+y^2} & \small \color{#3D99F6} \text{Note that }y = \sqrt 3 x \\ & = \frac {\sqrt 3 x}{2x^2-3x+4} = \frac {\sqrt 3}{2x-3+\frac 4x} \end{aligned}$

Note that $\tan \theta$ is maximum when $2x + \dfrac 4x$ is minimum. By AM-GM inequality , we have $2x + \dfrac 4x \ge 2 \sqrt{2x\cdot \dfrac 4x} = 4\sqrt 2$ . Equality occurs when $2x = \dfrac 4x$ or $x = \sqrt 2$ .

Then $AP = \dfrac x{\cos 60^\circ} = 2\sqrt 2 \approx \boxed{2.828}$ .