Slide
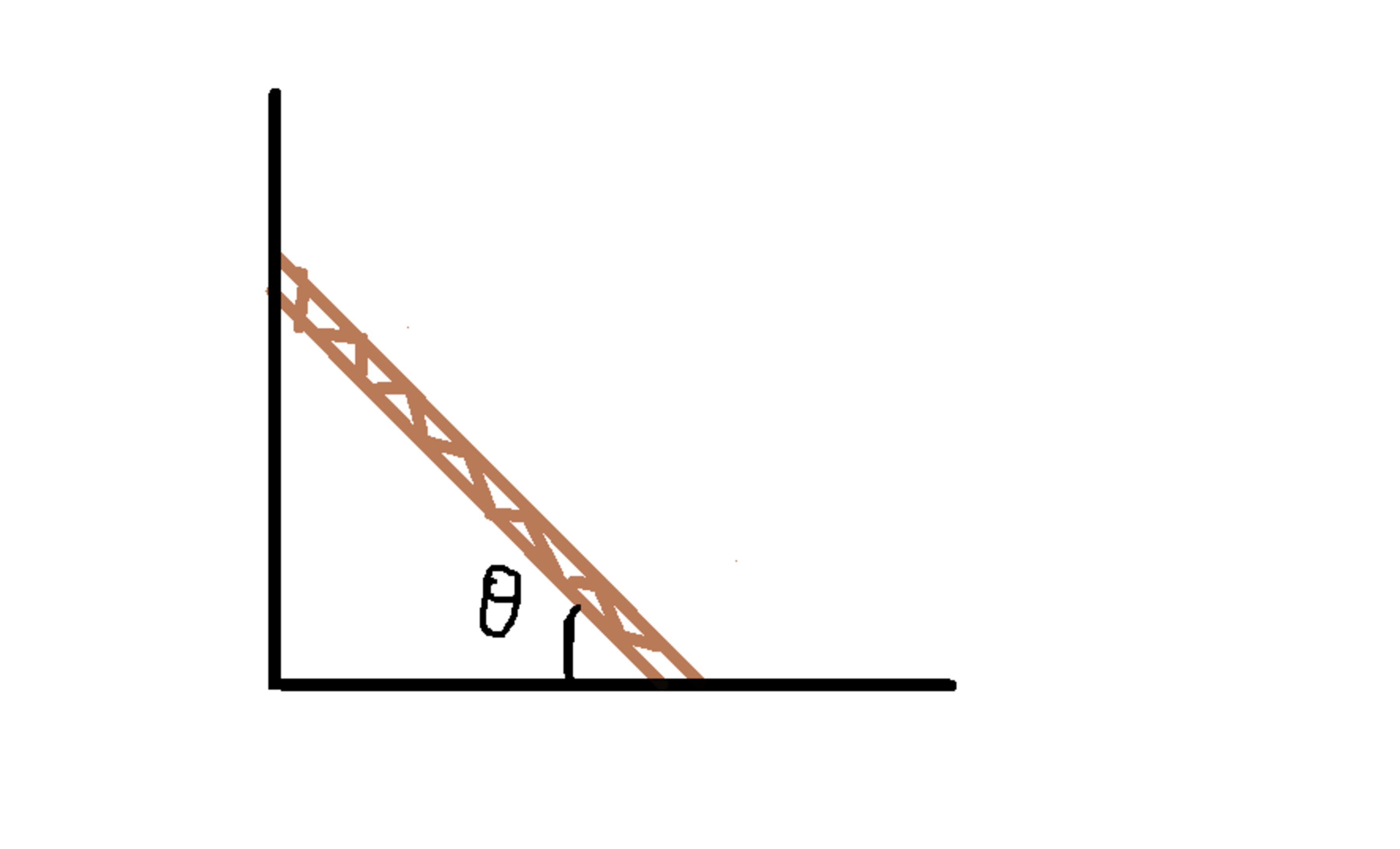 A uniform rod of mass M and
length L is resting between a
rough wall and a rough floor as
shown in the figure. The
coefficient of friction between any
two surface is
. For angle
for
which the rod is just on the verge
of slipping is
.
A uniform rod of mass M and
length L is resting between a
rough wall and a rough floor as
shown in the figure. The
coefficient of friction between any
two surface is
. For angle
for
which the rod is just on the verge
of slipping is
.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Photo to know the direction of reactions..
First start with conditions of stability ∑ F x = ∑ F y = ∑ M = 0 Let's assume that reaction at end point is the rod in vertical surface is R 1 and has distance X from horizontal surface , friction force equal to R 1 × μ we will also named it as F . And the reaction at end point of the rod at horizontal surface is R 2 and has distance S from the vertical surface , friction force equal to R 2 × μ . N o t e that t a n θ = S X
So we get from equations of equilibrium R 1 = R 2 × μ ( 1 ) R 2 + R 1 × μ = M from ( 1 ) we get R 2 = 1 + μ 2 M ( 2 ) Now we will take the Moment around point F we get R 2 × μ × X + M × 2 S = R 2 × S using ( 2 ) we have 1 + μ 2 M ∗ X ∗ μ + 2 M ∗ S = 1 + μ 2 M ∗ S Then dividing by S we get S X ∗ 1 + μ 2 μ = 1 + μ 2 1 − 2 1 Then S X = μ 1 − 2 μ 1 + μ 2 = 2 μ 1 − μ 2