Sliding block on a circular track with friction I
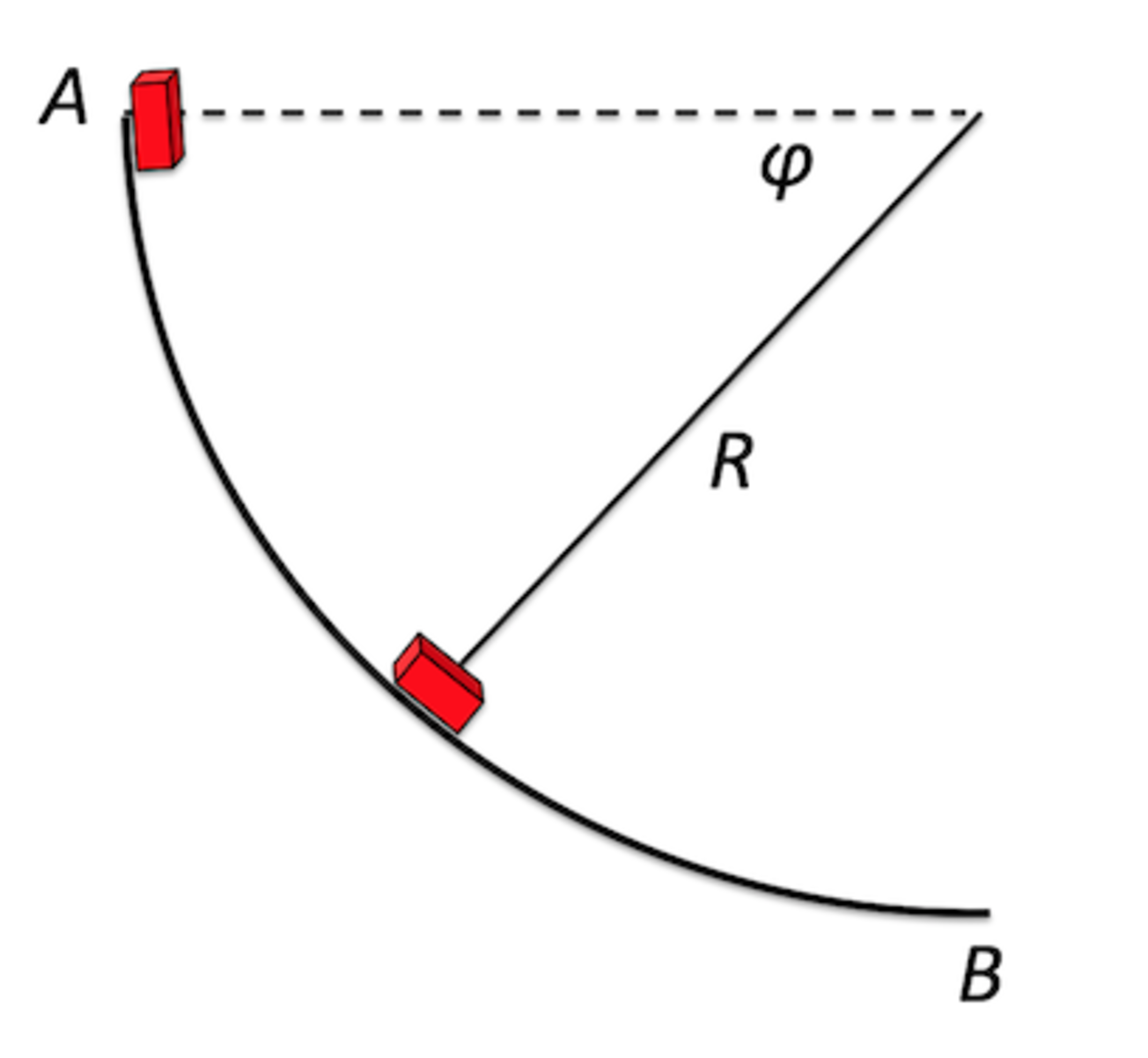
A small block having a mass
m
= 1.00 kg is released from rest on a circular track with radius
R
= 1.00 m. The block is released from point
A
at a height
R
above the floor and slides down along the surface. The coefficient of kinetic friction between the block and the surface is
μ
k
= 0.200. Find the velocity of the block (in m/s) when it gets to point
B
. Consider
g
= 9.81 m/s
2
The answer is 3.19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Amazing @Karan Chatrath!... I thought it could not be solved analytically!... Fabulous!...
Simulation code is attached. Note that x and v are the position and velocity along the circumference.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
|
Excellent!. :) Can you compute please the value of mu, such that the final velocity is zero?
3rd time was a charm for me on this one! Two algebra goofs discovered, and I was holding my breath on the 3rd attempt hoping my efforts weren’t in vain. I see that I am second to the party on this analytic solution, and my method is basically the same ( but a bit less clean) as @Karan Chatrath – but I’m going to go through my solution anyway because it took me a bit of effort.
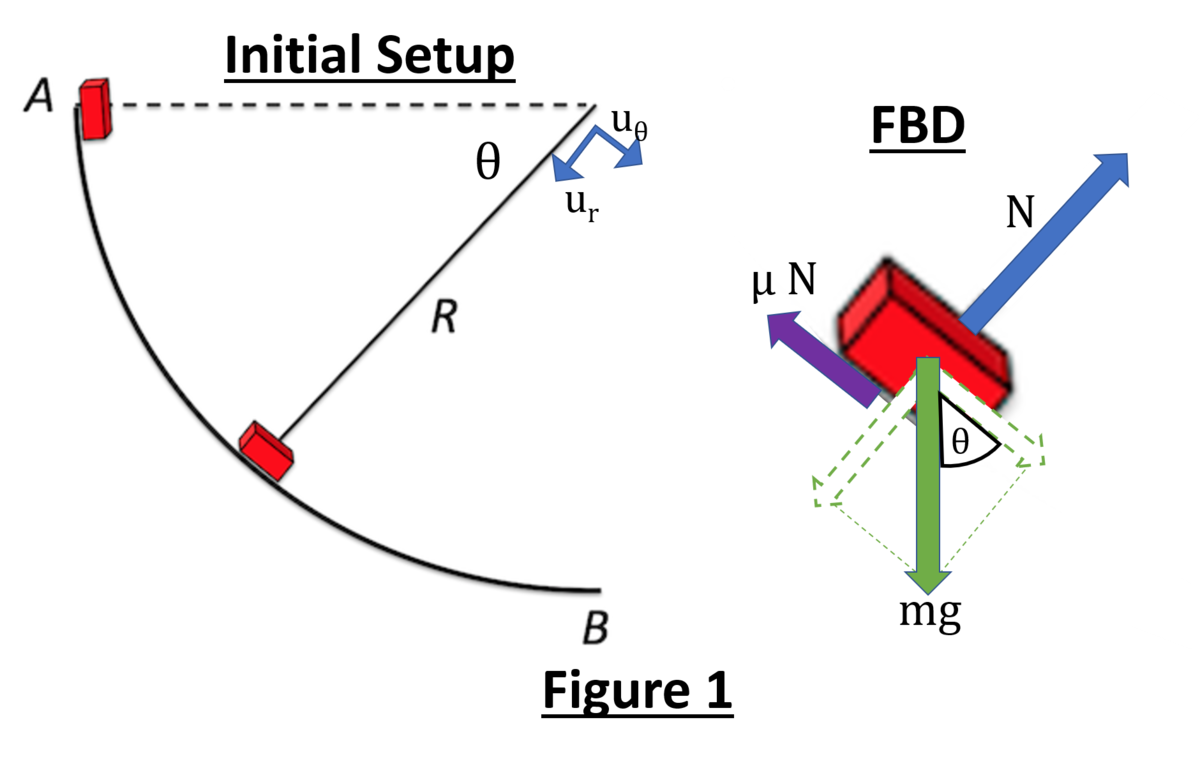
Figure 1 shows the initial setup. I chose to work in polar coordinates ( u r , u θ )
Firstly, I did some approximating to get some idea of the velocities. Neglecting friction entirely:
m g r = 2 1 m v 2
v = 2 g r = 4.43 s m
Then, I added a “rough” friction model where I make the normal force ( and friction force) constant by approximating its value at 4 π , neglecting friction to that point, and integrating it over the path.
v 4 π 2 ≈ 2 g r
N 4 π ≈ m g 2 2 + r m v 4 π 2
m g r = 2 1 m v 2 + ∫ F f r ⋅ d s
v ≈ m 2 ( m g r − μ N r 2 π ) = 2.56 s m
After establishing what I thought to be some reasonable bounds I felt comfortable enough to go after the solution.
So back to the solution using Newtons Second Law to formulate the equations of motion using the convention established in Fig 1:
∑ F u r = − N + m g sin θ = − m r θ ˙ 2 …Eq1
∑ F u θ = m g cos θ − μ N = m r θ ¨ …Eq2
Solve Eq1 for N and sub into Eq2, simplify:
r θ ¨ + μ r θ ˙ 2 = g ( cos θ − μ sin θ ) …Eq3
At this point I was not hopeful I would find an analytic result for the Second Order – Non Linear ODE. Then I remembered a “trick” from a similar problem involving air drag that would instead solve v ( θ , eliminating time from the equation.
Beginning the transformation:
v = r θ ˙ → θ ˙ = r v …Eq4
d t d v = r θ ¨ …Eq5
Substitute Eq4 & Eq5 into Eq3, simplify
d t d v + r μ v 2 = g ( cos θ − μ sin θ ) …Eq7
From here it seems just about as hopeless, but keeping on with the objective opens some doors on the following steps: Applying the Chain Rule and Subbing in Eq4.
d t d v = d θ d v d t d θ = d θ d v r v …Eq8
Changing Variables:
u = v 2 …Eq9
d v d u d θ d v = 2 v d θ d v = d θ d u …Eq10
Then, Substituting Eq9 and Eq10 into Eq7:
2 r 1 d θ d u + r μ u = g ( cos θ − μ sin θ ) …Eq11
We are left with a First Order Linear ODE in u ( v 2 )!
There are a few ways to tackle this, I chose solving the homogenous equation:
d θ d u + 2 μ u = 0 …Eq12
u h = C e − 2 μ θ …Eq13
Then add a particular solution that, in this case, essentially matches the RHS of Eq11 using the Method of Undetermined Coefficients. From the method, we are looking for a particular solution of the form:
u p = A cos θ + B sin θ …Eq14
And we sub Eq14 and Eq15 into Eq11 and determine the coefficients A and B algebraically in a term by term comparison:
u ’ p = − A sin θ + B cos θ …Eq15
u ’ p + 2 μ u p = g ( cos θ − μ sin θ ) …Eq16
This leads to a system of linear equations in A and B :
B + 2 μ A = 2 r g
2 μ B − A = − 2 μ r g
I find:
B = 2 r g ( 1 + 4 μ 2 1 − 2 μ 2 )
A = 2 μ r g ( 2 1 + 4 μ 2 1 − 2 μ 2 + 1 )
Then adjoin the solutions u h + u p , and use the initial conditions u ( 0 ) = 0 to find C ( the constant of integration leftover from Eq13).
u ( θ ) = C e − 2 μ θ + A cos θ + B sin θ
u ( 0 ) = 0 = C e − 2 μ 0 + A cos 0 + B sin 0 = C + A → C = − A
u ( θ ) = A ( cos θ − e − 2 μ θ ) + B sin θ
Then simply transform back to v by taking the square root.
v ( θ ) = A ( cos θ − e − 2 μ θ ) + B sin θ ...EOM
Lastly, plug in θ = 2 π
v ( 2 π ) ≈ 3.185 s m
and pheeeew….Thanks for the problem @Victor Robledo-Rella !
PS I do wonder, ( maybe its just my fragile ego ) but is this really a "level 2" problem? on the upside of a low rating; I guess if it was higher level I might not have attempted it...
Very nice and detailed solution. I agree that this problem should have been higher than level 2.
Log in to reply
Thanks Karan, I wrote my solution for someone ( like myself ) with a tenuous grasp on the subject matter ( which is why it has smaller mathematical jumps). Yours is the more elegant approach ( In my opinion ). I'm sure the last integration had its challenges! thanks for the positive response!
Congratulations @Eric Roberts!.... I'm glad you found the solution with a different method!... :) I love this community that connects people with similar interest over the world!..
Log in to reply
Thanks Victor! I have a BS in Mechanical Engineering Technology, out of college for nearly 8 years. I can honestly say, that I have learned much from this site. The background knowledge is sort of there ( I usually have to reference my old textbooks, put the stuff into the machine and turn the wheels to solve these types of differential equations) , but I have learned many techniques previously unknown right from the site. Overall, I agree its been a rewarding experience engaging with people that share a common interest in problem solving from across the globe!
Applying Newton 2nd law to this problems, yields an interesting equation!... When the velocity of the block increases as it goes down, the normal force exerted by the surface increases (since it depends on v 2 ), hence the friction force on the block increases as well, reducing thus its velocity!... I solved numerically the equation for its velocity as function of the angle ϕ , assuming its tangential acceleration is constant within a very small interval Δ t ). I would love to see your solution!... :)
@Steven Chase shows a numerical route to the answer but I have attempted an analytical approach. A bulk of this solution is even used to solve part 2 of this set.
Let the coordinates of the block be:
x = − R cos ϕ y = − R sin ϕ
Computing time derivatives:
x ˙ = R ϕ ˙ sin ϕ y ˙ = − R ϕ ˙ cos ϕ
Therefore, the speed of the block is:
v = x ˙ 2 + y ˙ 2 = R ϕ ˙
x ¨ = R ϕ ¨ sin ϕ + R ϕ ˙ 2 cos ϕ y ¨ = − R ϕ ¨ cos ϕ + R ϕ ˙ 2 sin ϕ
Let the normal force acting on the block due to contact with the circular surface be N at point P directed towards the centre of the circle. The friction force acting on the block is f = μ N acting tangentially to the circular surface against the block's motion.
The equations of motion along X and Y can be computed as such:
m x ¨ = N cos ϕ − μ N sin ϕ m y ¨ = N sin ϕ + μ N cos ϕ − m g
Replacing the double derivative terms and eliminating N from the above two equations after some simplification gives the equation of motion:
ϕ ¨ + μ ϕ ˙ 2 = R g ( cos ϕ − μ sin ϕ ) = f ( ϕ )
Since the block starts from rest, ϕ ( 0 ) = ϕ ˙ ( 0 ) = 0 .
The differential equation:
ϕ ¨ + μ ϕ ˙ 2 = f ( ϕ ) ϕ ˙ d ϕ d ϕ ˙ + μ ϕ ˙ 2 = f ( ϕ ) 2 ϕ ˙ d ϕ d ϕ ˙ + 2 μ ϕ ˙ 2 = 2 f ( ϕ )
Multiplying both sides by e 2 μ ϕ gives:
e 2 μ ϕ 2 ϕ ˙ d ϕ d ϕ ˙ + 2 μ e 2 μ ϕ ϕ ˙ 2 = 2 f ( ϕ ) e 2 μ ϕ
d ϕ d ( ϕ ˙ 2 e 2 μ ϕ ) = 2 f ( ϕ ) e 2 μ ϕ
Now, separating and integrating (and applying initial conditions) gives:
ϕ ˙ 2 e 2 μ ϕ = ∫ 0 ϕ 2 f ( x ) e 2 μ x d x
Where f ( x ) = R g ( cos x − μ sin x )
Solving this tedious integral and simplifying gives:
ϕ ˙ = ( R 2 g ( − 4 μ 2 + 1 ( 2 μ 2 − 1 ) sin ( ϕ ) − 3 μ cos ( ϕ ) − 4 μ 2 + 1 3 μ e − 2 μ ϕ ) ) 1 / 2
Given that R = 1 and therefore: v = ϕ ˙ and μ = 0 . 2 , and also the fact that the speed is to be computed when ϕ = π / 2 gives the answer by substituting all this into the result above. The answer is:
v ( π / 2 ) ≈ 3 . 1 8