Sliding block on a circular track with friction II
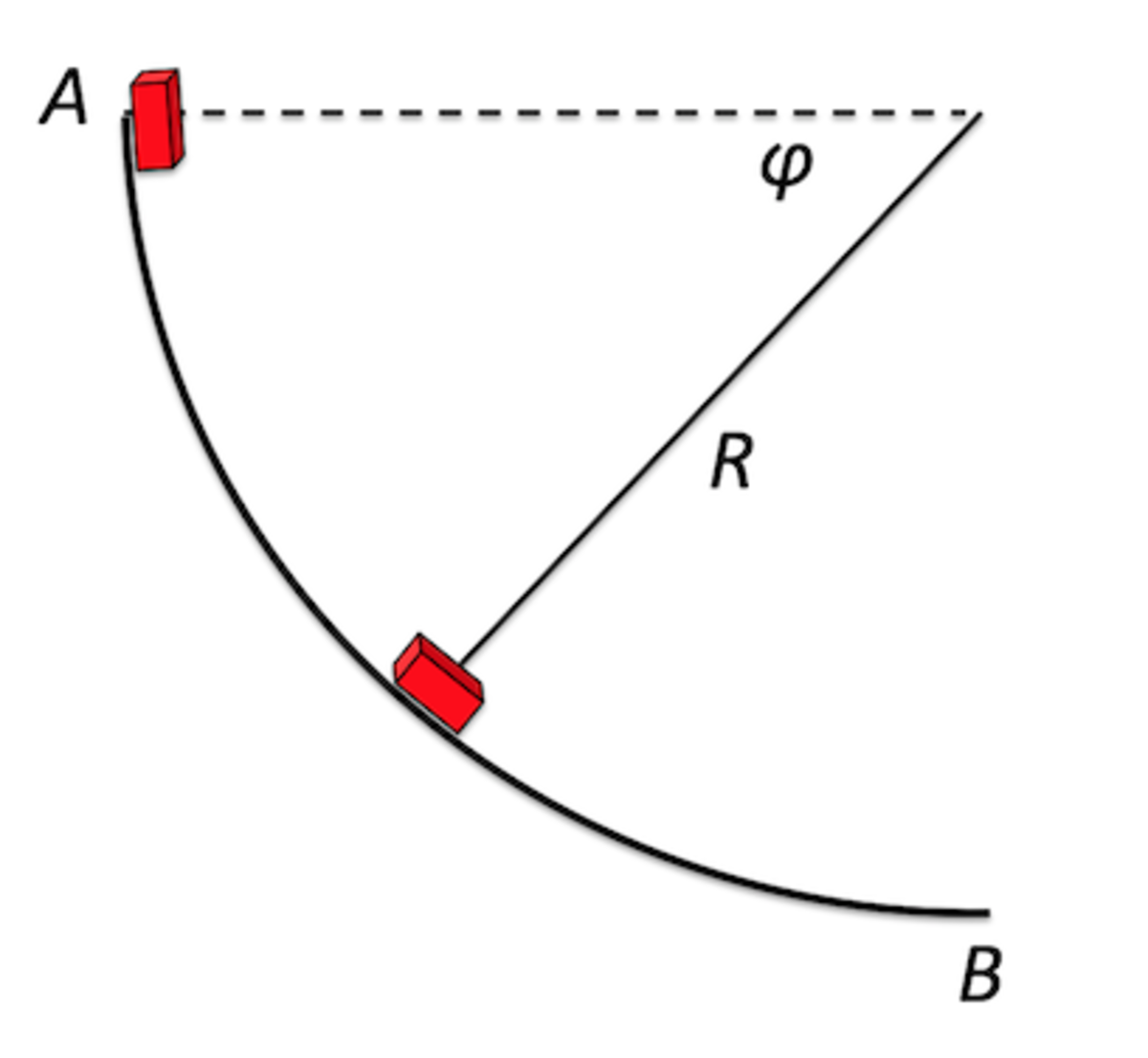
A small block having a mass
m
= 1.00 kg is released from rest on a circular track with radius
R
= 1.00 m. The block is released from point
A
at a height
R
above the floor and slides down along the surface. Find the exact coefficient of kinetic friction
that would stop the block exactly when it reaches point
B
. Consider
g
= 9.81 m/s
.
(I found
= 0.604016)
The answer is 0.605.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the coordinates of the block be:
x = − R cos ϕ y = − R sin ϕ
Computing time derivatives:
x ˙ = R ϕ ˙ sin ϕ y ˙ = − R ϕ ˙ cos ϕ
Therefore, the speed of the block is:
v = x ˙ 2 + y ˙ 2 = R ϕ ˙
x ¨ = R ϕ ¨ sin ϕ + R ϕ ˙ 2 cos ϕ y ¨ = − R ϕ ¨ cos ϕ + R ϕ ˙ 2 sin ϕ
Let the normal force acting on the block due to contact with the circular surface be N at point P . The friction force acting on the block is f = μ N acting tangentially to the circular surface against the block's motion.
The equations of motion along X and Y can be computed as such:
m x ¨ = N cos ϕ − μ N sin ϕ m y ¨ = N sin ϕ + μ N cos ϕ − m g
Replacing the double derivative terms and eliminating N from the above two equations after some simplification gives the equation of motion:
ϕ ¨ + μ ϕ ˙ 2 = R g ( cos ϕ − μ sin ϕ ) = f ( ϕ )
Since the block starts from rest, ϕ ( 0 ) = ϕ ˙ ( 0 ) = 0 .
The differential equation:
ϕ ¨ + μ ϕ ˙ 2 = f ( ϕ ) ϕ ˙ d ϕ d ϕ ˙ + μ ϕ ˙ 2 = f ( ϕ ) 2 ϕ ˙ d ϕ d ϕ ˙ + 2 μ ϕ ˙ 2 = 2 f ( ϕ )
Multiplying both sides by e 2 μ ϕ gives:
e 2 μ ϕ 2 ϕ ˙ d ϕ d ϕ ˙ + 2 μ e 2 μ ϕ ϕ ˙ 2 = 2 f ( ϕ ) e 2 μ ϕ
d ϕ d ( ϕ ˙ 2 e 2 μ ϕ ) = 2 f ( ϕ ) e 2 μ ϕ
Now, separating and integrating (and applying initial conditions) gives:
ϕ ˙ 2 e 2 μ ϕ = ∫ 0 ϕ 2 f ( x ) e 2 μ x d x
Where f ( x ) = R g ( cos x − μ sin x )
Solving this tedious integral and simplifying gives:
ϕ ˙ = ( R 2 g ( − 4 μ 2 + 1 ( 2 μ 2 − 1 ) sin ( ϕ ) − 3 μ cos ( ϕ ) − 4 μ 2 + 1 3 μ e − 2 μ ϕ ) ) 1 / 2
Now, given that R = 1 the speed of the block v = ϕ ˙ . For this to be zero at ϕ = π / 2 , the above expression on the right hand side must be evaluated at ϕ = π / 2 and equated to zero. On simplification, this given the following non-linear equation:
1 − 2 μ 2 3 μ = e π μ
This equation can be solved numerically to obtain the solution of approximately:
μ ≈ 0 . 6 0 3