Sliding box

Classical Mechanics Level 5

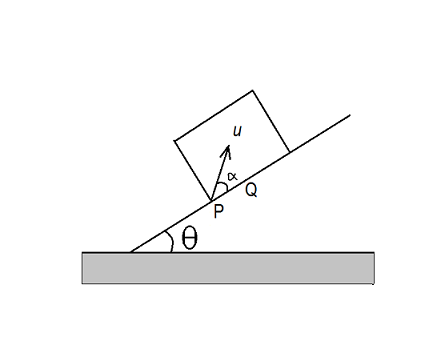
A large heavy box is siding without friction down a smooth inclined plane of inclination $\theta$ . From a point P on the bottom of the box a particle is projected inside the box, with speed $u$ (relative to box) at angle $\alpha$ with the bottom of the box. If horizontal displacement of the particle with respect to the ground is zero, find the speed of the box with respect to the ground at the moment when the particle was projected. Answer upto 3 decimal places

Take $\theta$ = 30°, $\alpha$ = 30° , $u$ = 10m/s and $g$ = 10m/s².

The answer is 5.7735.

2 solutions

Steven Chase
Mar 14, 2017

This is a velocity superposition problem. The net horizontal component of the velocity is zero. Mathematically, this means:

$\large{V_{box} \, cos(\theta - 180^\circ) + u \, cos(\theta + \alpha) = 0 \\ V_{box} \, cos(30^\circ - 180^\circ) + u \, cos(30^\circ + 30^\circ) = 0 \\ V_{box} \, cos(-150^\circ) + u \, cos(60^\circ) = 0 \\ V_{box} \frac{-\sqrt{3}}{2} + 10 \frac{1}{2} = 0 \\ V_{box} = \frac{10}{\sqrt{3}} \approx 5.7735}$

James Pohadi
Aug 29, 2017

Horizontal velocity of the box with respect to the ground $=v_{b,g,x}=-v_{b,g} cos\theta$

Horizontal velocity of the particle with respect to the box $=v_{p,b,x}=u cos(\alpha+\theta)$

Since the horizontal displacement of particle with respect to ground is $0$ , then, the horizontal velocity of the particle with respect to the ground $v_{p,g,x}$ also $0$

$\begin{aligned} \implies v_{p,g,x}&=v_{p,b,x}+v_{b,g,x} \\ 0&=u cos (\alpha+\theta)+(-v_{b,g} cos \theta) \\ v_{b,g} cos \theta&=u cos (\alpha+\theta) \\ v_{b,g} &=\frac {u cos (\alpha+\theta)}{cos\theta} \\ v_{b,g} &=\frac {10 cos (30+30)}{cos 30} \\ v_{b,g} &=\boxed {\frac {10}{\sqrt {3}}} \end{aligned}$

Sliding box

The answer is 5.7735.

2 solutions

0 pending reports