Sliding coins

Logic Level 3

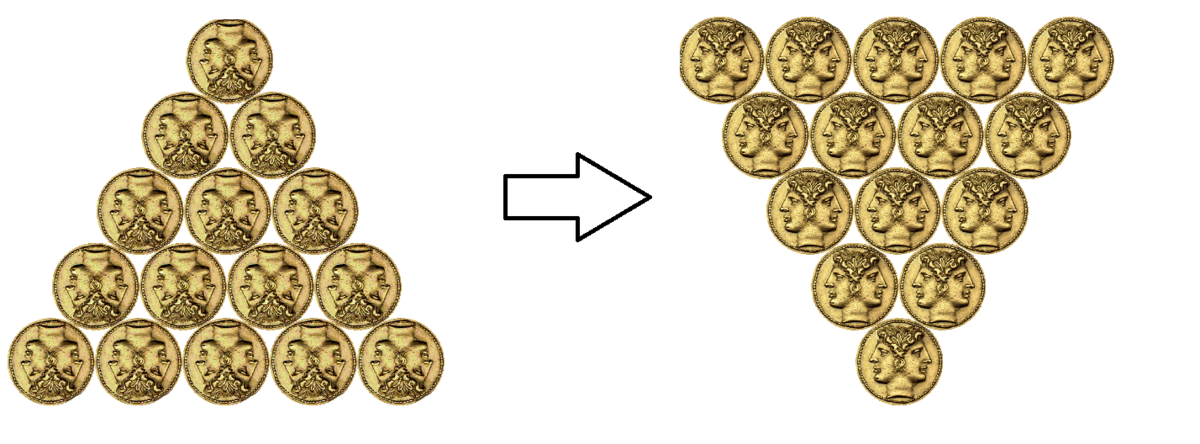
What is the minimum number of moves required to change the arrangement at the left to the right consisting of 15 coins by sliding one coin at a time to a different position in which it touches two other coins?

Note: Generalize this.

Details And Assumptions :

  • Neglect the design inscribed on the coin and consider all coins to be plain.
  • You cannot lift the coins.
4 7 6 5 3 8

Nihar Mahajan by Nihar Mahajan , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Nihar Mahajan
Jul 1, 2015

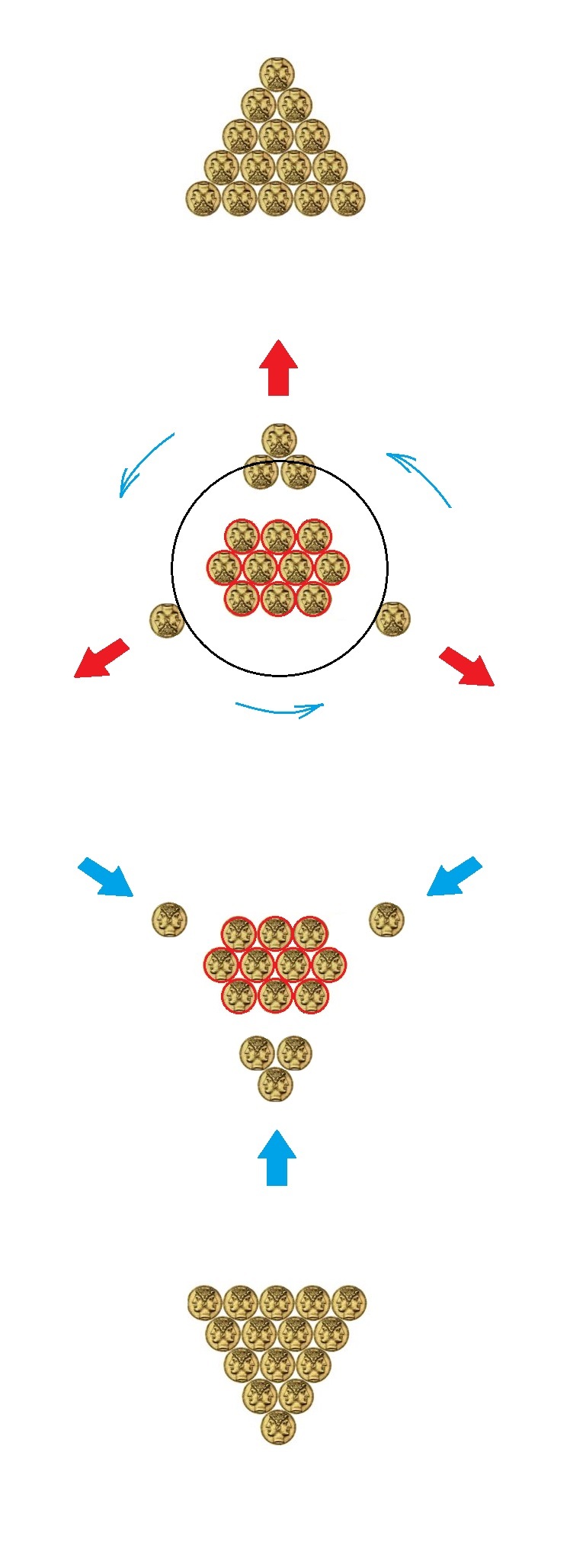
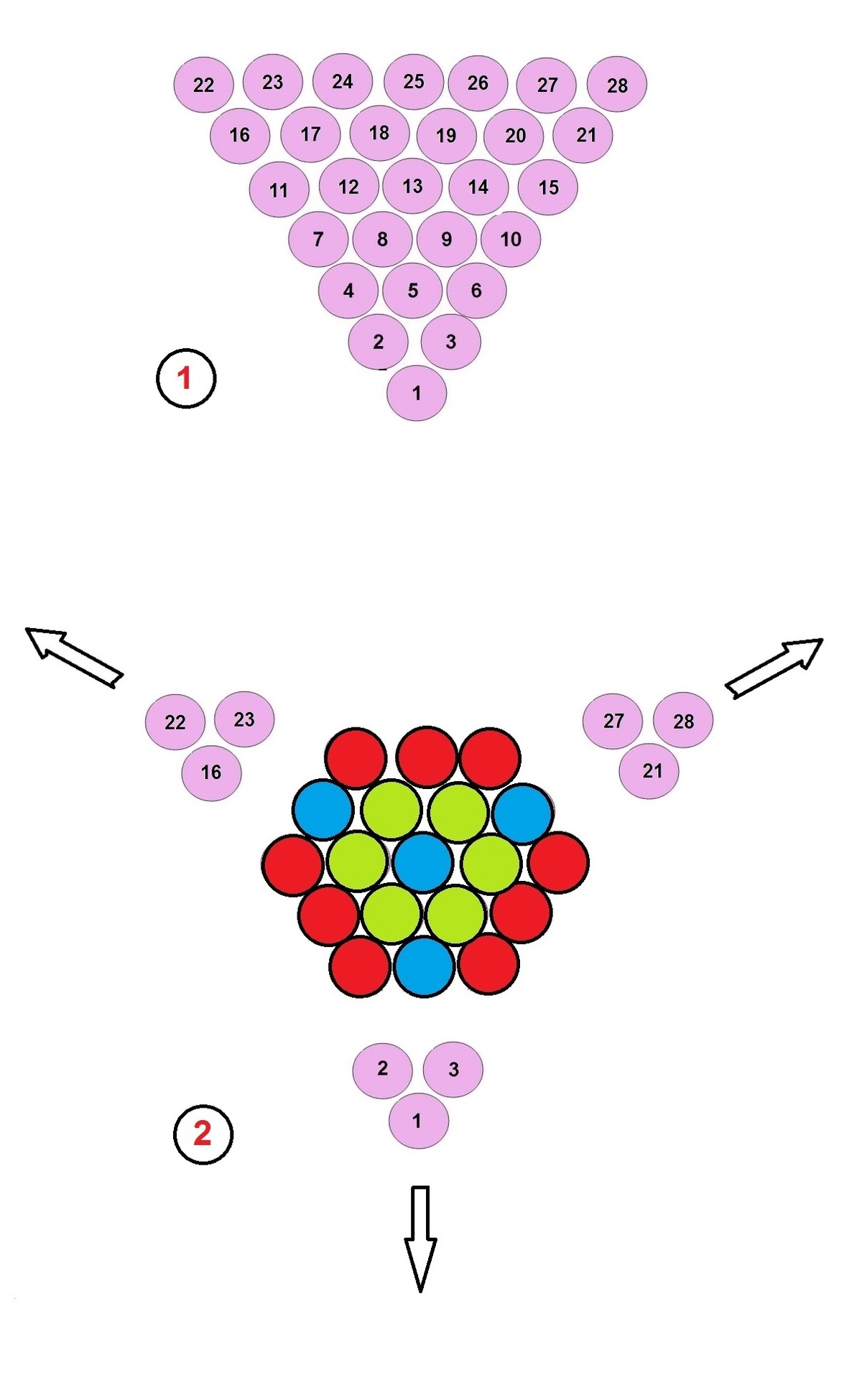
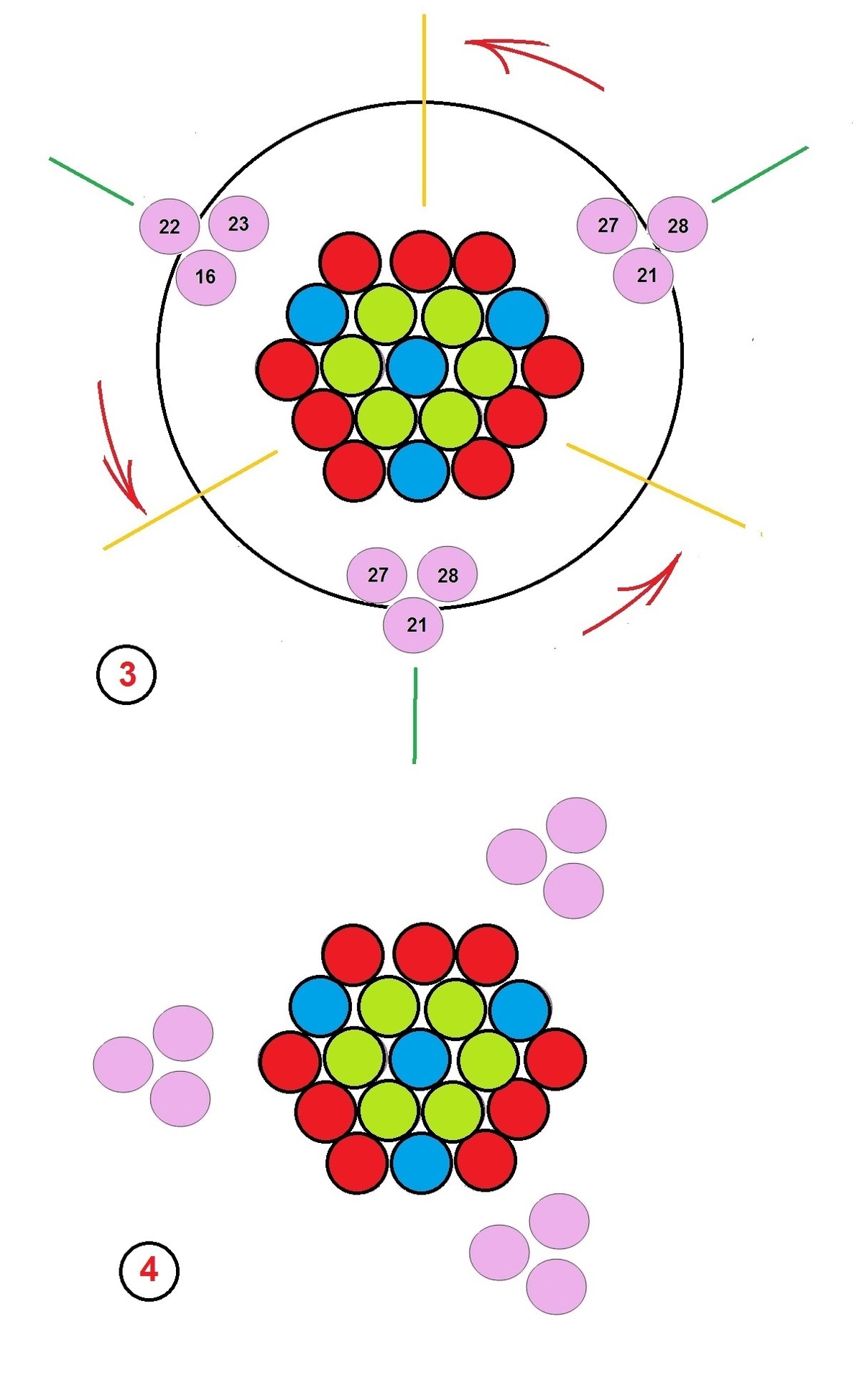
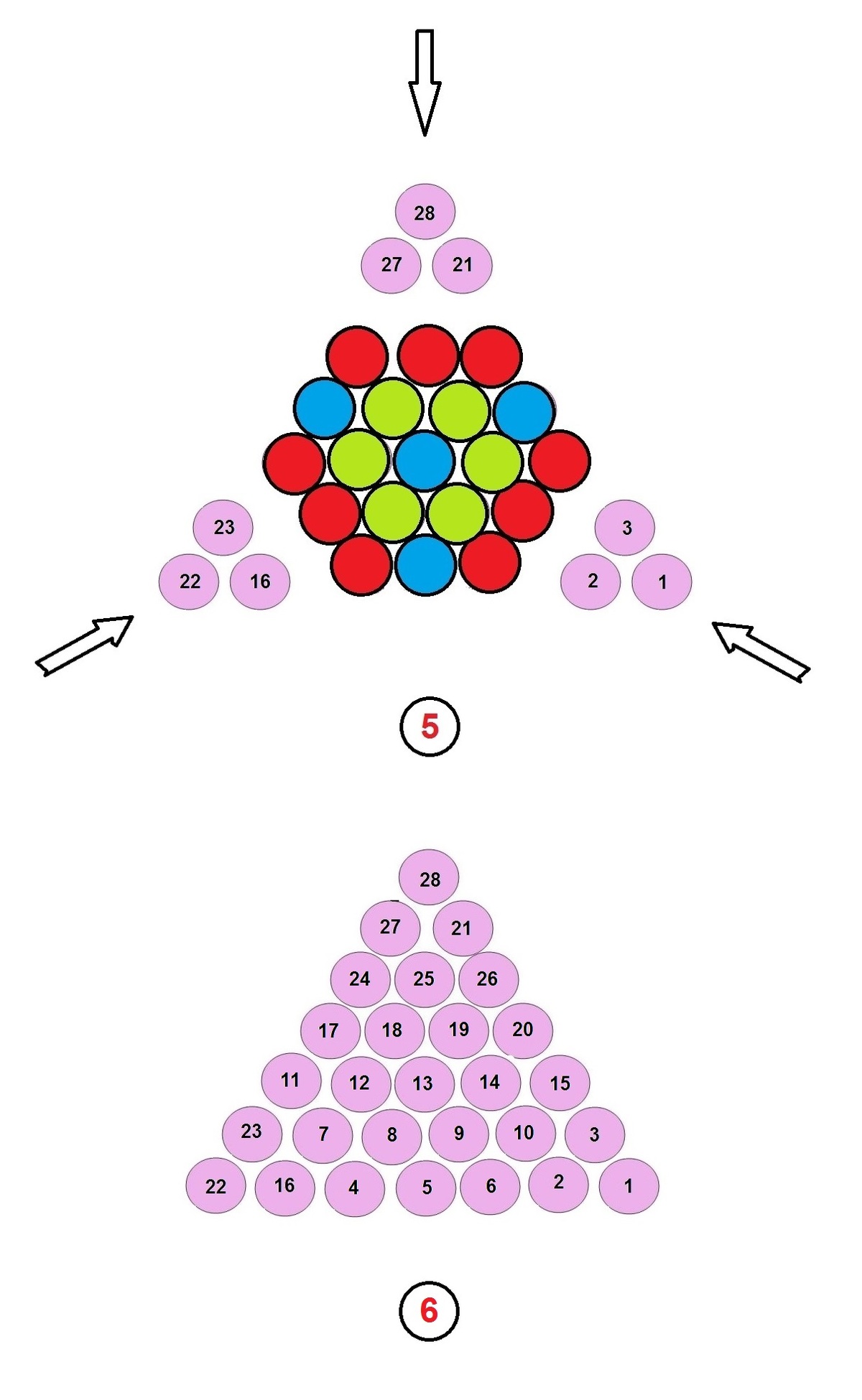
In the image , let the red circles be touching.

3 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Can you prove that it's minimum? Hint: See Prasun Biswas' note .

Ahmed Obaiedallah
Jul 11, 2015

Well to solve this kind of problems I try first to determine the part that won't move and I found out in such problems it's a hexagon core (regular or irregular) ,

Then I just pop the moving parts out and kind of imagine myself rotating them around a circle then push them back in their new position

Here is another one with bigger triangle (28 coins) that has a regular hexagon in it's core (because it's more understandable with a regular hexagon core)

Also notice the inner 10 coins triangle it has a regular hex core as well I gave it a different color so you can recognize it easily

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...