Sliding down a sliding incline - 2
A 1-kg block is initially at the top of a frictionless, inclined plane that is part of a sliding wedge of mass 10 kg. The system is initially at rest, and then the block is released. As it slides down the incline, the wedge slides horizontally on the frictionless stationary floor. It is given that the horizontal span of the base of the wedge is 220 cm and that the angle that the inclined plane makes with the horizontal is
Find the total distance in centimeters that the wedge moves (with respect to the stationary floor) as the block slides down the inclined surface from the top to the bottom.
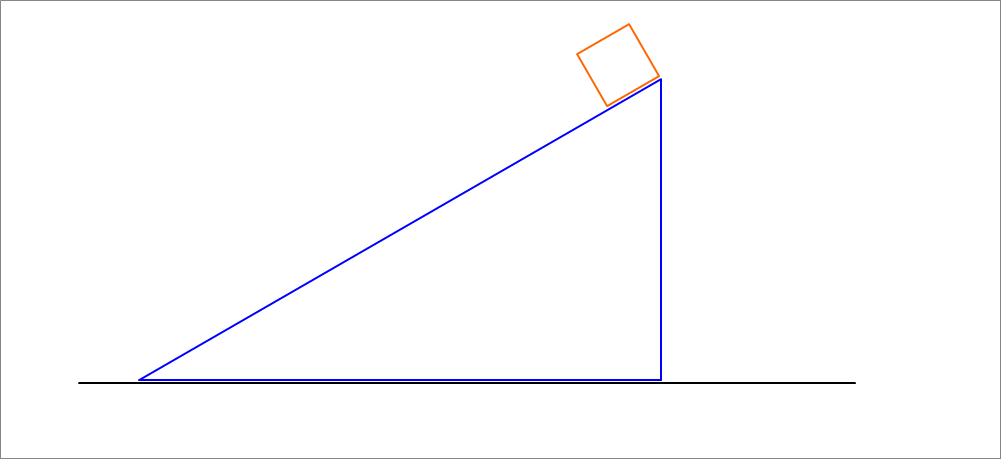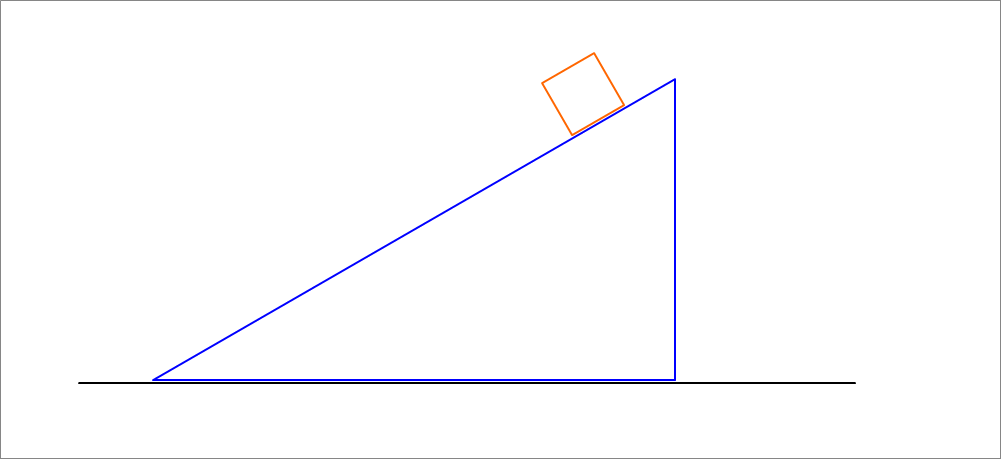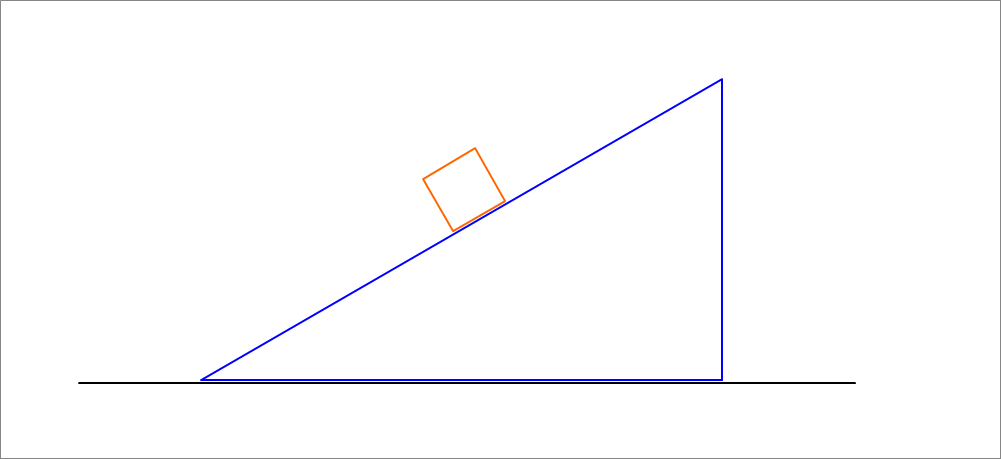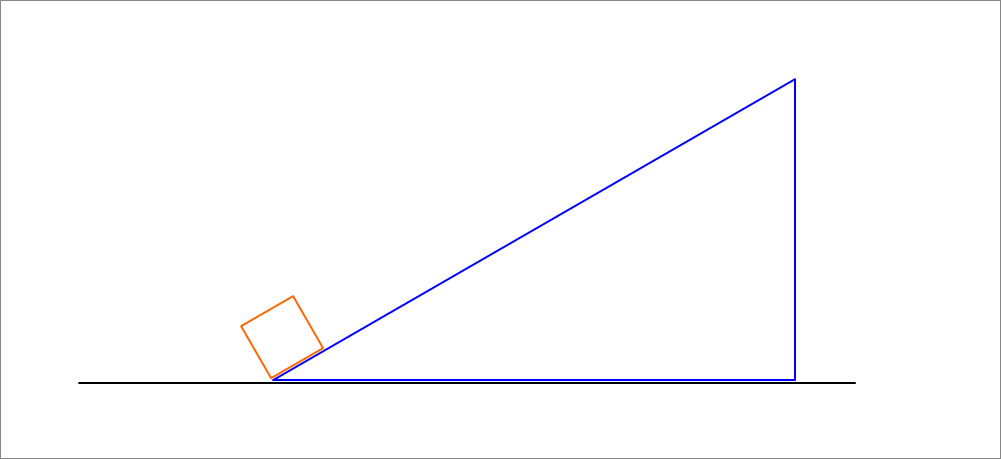
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Figure 1. is a snapshot in time of the initial setup.
There are two frames of reference X 1 , Y 1 attached to the incline, and X 2 , Y 2 fixed to the ground. X 1 , Y 1 is non-inertial and the force balance with respect to the block must include inertial terms to account for this. The Free Body Diagram of the incline is shown in Figure 2.
In the absence of friction we only need consider the equation of motion in X 2 . The equation of motion is given by:
∑ F x 2 = M x 2 ¨ = N sin θ ...Eq1
Now turn to Figure 3., the Free Body Diagram of the Block.
The form of Newtons Law with non-inertial frames is given by m r ¨ = F − m A
∑ F x 1 = m x 1 ¨ = m g sin θ + m x 2 ¨ c o s θ ...Eq2
The last term on the right is the negative of the projection a 2 → a 1 . If you imagine we are riding on the block we are going to feel an additional inertial force pulling us down the incline. The same way when you accelerate forward in a car you are pushed back into the seat and visa versa.
Moving on to the force balance in Y 1 . There is no acceleration in the Y 1 direction. The force balance on the block in this direction given by:
∑ F y 1 = 0 = N − m g cos θ + m x 2 ¨ s i n θ ...Eq3.
Now we have these three equations of motion, that we can solve to find x 2 ¨ and x 1 ¨ .
Solving for N in Eq3.
N = m g cos θ − m x 2 ¨ s i n θ
Substitute N into Eq1. and solve for x 2 ¨ and simplify.
x 2 ¨ = M + m sin 2 θ m g sin θ cos θ
Then take that result and substitute into Eq2. and simplify using a common denominator.
x 1 ¨ = M + m sin 2 θ ( M + m ) g sin θ
Next, we need to figure out how long the force from the block is applied to the incline. All accelerations are constant, so we can just use kinematic relationships with the initial velocity of the block is zero, and the distance traveled down the incline l
l = 2 1 x 1 ¨ t 2 = 2 1 ( M + m sin 2 θ ( M + m ) g sin θ ) t 2
or
t 2 = ( M + m ) g sin θ 2 l ( M + m sin 2 θ )
Similarly, Δ x 2 is found by substituting t 2 , and simplifying. letting l = c o s θ b where b is the length of the base.
Δ x 2 = 2 1 x 2 ¨ t 2 = 2 1 ( M + m sin 2 θ m g sin θ cos θ ) ( ( M + m ) g sin θ 2 l ( M + m sin 2 θ ) ) = ( M + m m ) b
Finally, plugging in values Δ x 2 = 2 0 cm