Sliding Ellipse

Geometry Level 5

Consider an ellipse whose semi-axes have lengths $a$ and $b$ where $a>b$ . The ellipse slides along the coordinate axes as shown in the figure. Find the area of the closed curve traced by the foci of the ellipse.

\pi(a^2-b^2)

\dfrac{\pi ab(a-b)}{a+b}

\pi(a-b)^2

\dfrac{\pi ab(a^2-b^2)}{a^2+b^2}

2 solutions

Digvijay Singh
May 23, 2021

The orthogonal coordinate axes can be thought to be two perpendicular tangents to the ellipse. The origin, therefore, lies on the director circle of the ellipse which is centered at $C$ with radius $\sqrt{a^2+b^2}$ . Hence we know that the center $C$ of the ellipse lies at a constant distance of $\sqrt{a^2+b^2}$ from the origin. The locus of $C$ is a part of arc of the circle $x^2+y^2=a^2+b^2$ , and the area $A'$ enclosed by this locus is hence $0$ .

Now, the line segment $F_1 F_2$ can be thought to be a chord sliding inside the closed curve traced by its end points. Using Holditch's theorem , we know that the difference between the area $A$ enclosed by the required locus and the area $A'$ enclosed by the locus of point $C$ must be equal to $\pi pq$ where $p$ and $q$ are the distances of $C$ from $F_1$ and $F_2$ .

We know that $p=q=\sqrt{a^2-b^2}$ , hence $\boxed{A-A'=A=\pi(a^2-b^2)}$ .

This is a really nice problem - thanks for sharing it! You inspired me to look into some variations; I don't think I'll have time to get to posting all the problems I would like to before the community closes, so here are a couple I don't have answers to based on yours.

If instead of looking at the foci, we consider the region swept out by the entire ellipse, we can get a few qualitatively different shapes. With semiaxes $a=3$ and $b=2$ , the region is as follows:

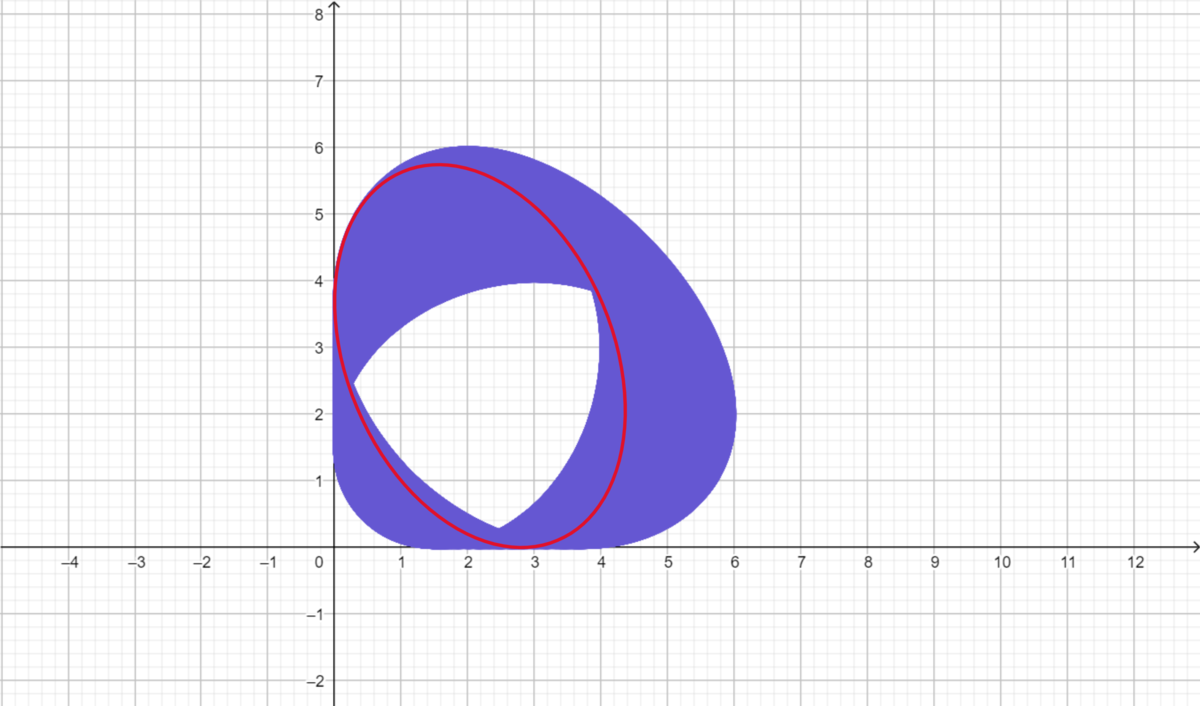
What can we say about this shape? For instance, how large is the blue area? How large is the hole in the middle? Is there a "nice" equation for either the inner or outer boundary curve?

Here's the GeoGebra page I made to generate the above diagram; you can see the effect of varying $a,b$ there. (Press the play button on the slider to draw the region)

Chris Lewis - 4 days, 11 hours ago

Well, I tried to find a nice equation for the envelope but the intermediate equations are just too complicated to solve.

Take $h=\sqrt{a^2\cos^2{\theta}+b^2\sin^2{\theta}}$ and $k=\sqrt{a^2\sin^2{\theta}+b^2\cos^2{\theta}}$

Consider $F(x,y,\theta)=k^2(x-h)^2-(a^2-b^2)(x-h)(y-k)\sin(2\theta)+h^2(y-k)^2-a^2b^2$

Then the equation of the envelope is given by the two simultaneous equations: $F(x,y,\theta)=0$ and $\dfrac{\partial}{\partial\theta}F(x,y,\theta)=0$

It is not easy to eliminate $\theta$ from the above two equations to get an equation in terms of $x$ and $y$ only, I couldn't do it.

I did, however, notice the fact that, there exists a constant $\lambda\approx3.384$ such that for ellipses in which $\dfrac{a}{b}>\lambda$ , the hole in the middle disappears.

Digvijay Singh - 4 days, 5 hours ago

Ryan S
May 25, 2021

Someone unfamiliar with Holditch's theorem might have used a combination of deduction and intuition to not necessarily solve the problem, but still answer it:

First, let $a$ approach infinity and $b=\frac1a$ . Visually, the foci-traced figure in the limit will resemble arbitrarily better and better, a quarter of a circle, with radius $2a$ , the area of which is therefore $\frac14\pi(2a)^2=\pi a^2$ . Only options $\pi(a^2-b^2)$ and $\pi(a-b)^2$ demonstrate this limit.

Second, when you dilate the graph, scaling as a result, $a$ and $b$ by a factor of some $x$ , the area of the traced figure must scale by $x^2$ . From the remaining possible answers, only $\pi(a^2-b^2)$ fits this description. Since there are no more possible answers, as far as the someone is concerned, this is the correct one.

The subtle approach would be to parameterize the family of ellipses and then find the locus traced by the foci. The locus of the foci turns out to be the curve ${(x^2+y^2)(x^2 y^2+b^4)=4a^2 x^2 y^2}$ , and its area can be found by common calculus techniques.

Digvijay Singh - 2 weeks, 4 days ago

The scaling property is satisfied by all the options. So your final point is actually wrong.

Digvijay Singh - 2 weeks, 4 days ago

Yup - @Digvijay Singh always picks very plausible answer options! (Which is a real art - I've noticed this in your other problems too and meant to mention it, very deft.)

That said, it is a useful approach to check how sensible the options are; it's a useful skill, because you can also apply it to questions that aren't multiple choice to verify your answer.

Chris Lewis - 2 weeks, 4 days ago

Sliding Ellipse

2 solutions

0 pending reports