Sliding linked blocks
If the slider block A is moving downward at
V
a
= 4 m/s, determine the magnitude of velocity of block
B at the instant shown.
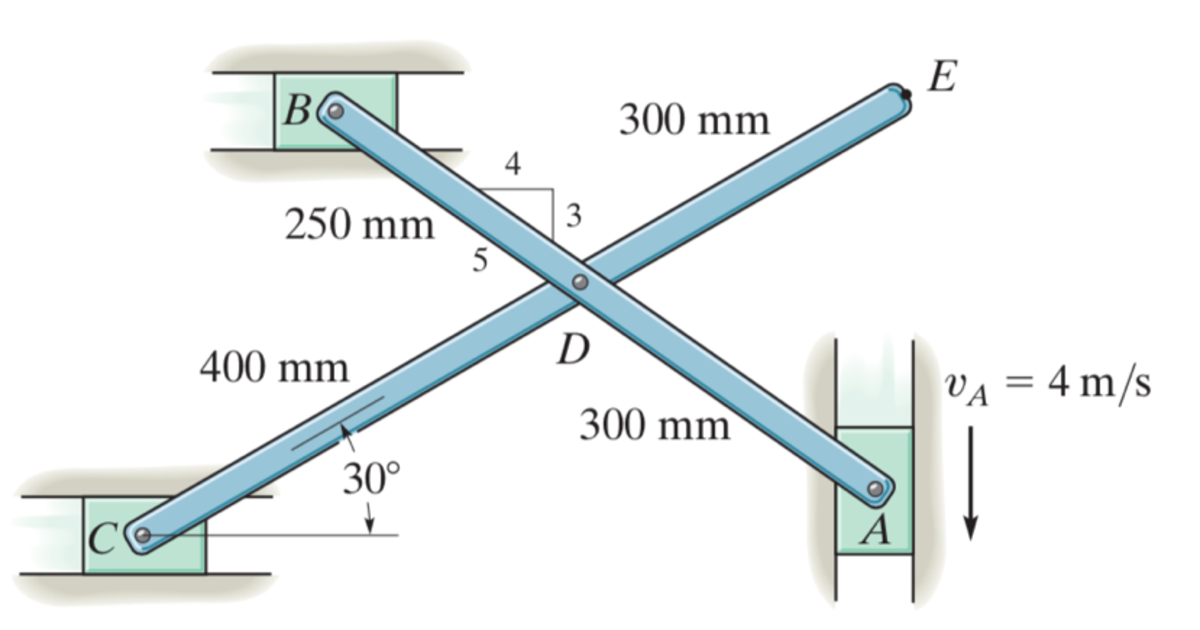
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thanks for the solution.
Let the length of the rod AB be l and the angle it subtends with horizontal be α . Then V a = l c o s α d t d α = 4 . This implies l d t d α = 5 (since c o s α = 5 4 ). Then ∣ V b ∣ = l s i n α d t d α = 3 (since s i n α = 5 3 )
Thanks for the solution.
( A x − B x ) 2 + ( A y − B y ) 2 = L A B 2
Time-differentiating both sides:
( A x − B x ) ( A ˙ x − B ˙ x ) + ( A y − B y ) ( A ˙ y − B ˙ y ) = 0 ( A x − B x ) ( 0 − B ˙ x ) + ( A y − B y ) ( A ˙ y − 0 ) = 0
It is easy to calculate ( A x , B x , A y , B y ) with respect to point D using the information given. All that remains is to re-arrange and solve for B ˙ x , which turns out to be 3