Sliding on a Parabolic Block

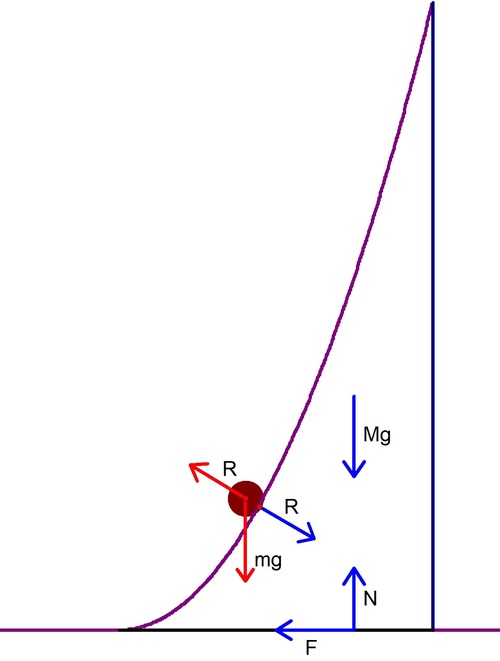
It might be clearer to do the general theory in the abtract before getting down to specifics. Suppose that the cross-section of the block is given by the equation $y = f(x)$ for $x \ge 0$ where $f$ is a continuously differentiable function such that $f(0) = f'(0) = 0$ and $f'(x) \ge 0$ , $f''(x) \ge 0$ for all $x \ge 0$ . Suppose that the block has mass $M = \lambda m$ , where $\lambda > \tfrac12$ .

Assume that the curve remains stationary throughout the motion. The the position vector, velocity and acceleration of the particle are given by $\mathbf{r} \; = \; \binom{x}{f(x)} \hspace{1cm} \dot{\mathbf{r}} \; = \; \binom{1}{f'(x)}\dot{x} \hspace{1cm} \ddot{\mathbf{r}} \; = \; \binom{1}{f'(x)}\ddot{x} + \binom{0}{f''(x)}\dot{x}^2$ If the particle experiences a normal reaction $\mathbf{R}$ from the curve, then $\mathbf{R} = m\rho\binom{-f'(x)}{1}$ for some $\rho > 0$ , and so the equation of motion of the particle is $\binom{1}{f'(x)}\ddot{x} + \binom{0}{f''(x)}\dot{x}^2 \; = \; \rho\binom{-f'(x)}{1} + g\binom{0}{-1}$ Taking components of this equation tangential and normal to the curve, we obtain the equations $\begin{aligned} \big[1 + f'(x)^2\big]\ddot{x} + f'(x)f''(x)\dot{x}^2 + gf'(x) & = \; 0 \\ f''(x)\dot{x}^2 + g & = \; \rho\big[1 + f'(x)^2\big] \end{aligned}$ Integrating the first of these equations gives $\tfrac12\big[1 + f'(x)^2\big]\dot{x}^2 + gf(x) \; = \; \tfrac12v^2$ and so $0 \; < \; \rho \; = \; \frac{g + f''(x)\dot{x}^2}{1 +f'(x)^2} \; = \; \frac{g\big[1 + f'(x)^2\big] + f''(x)\big[v^2 - 2gf(x)\big]}{\big[1 +f'(x)^2\big]^2}$ In addition to the reaction from the bead and gravity, the block is acted upon by a normal reaction $N$ and a friction force $F$ from the ground, and hence we must have $m\rho\binom{f'(x)}{-1} + \lambda mg\binom{0}{-1} + \binom{-F}{N} \; = \; \mathbf{0}$ and hence $N \; = \; m\big(\lambda g + \rho\big) \hspace{2cm} F \; = \; m\rho f'(x)$ and so this motion is only possible provided that $\rho f'(x) \,\le\, \mu\big(\lambda g + \rho)$ at all times, so that $\mu \ge \frac{\rho f'(x)}{\lambda g + \rho}$ For this problem we have $f(x) \,=\, \tfrac{1}{2a}x^2$ . If we write $X = v\sqrt{\tfrac{a}{g}}$ , then these equations reduce to $\tfrac12\big[1 + \tfrac{x^2}{a^2}\big] \dot{x}^2 \; = \; \tfrac{g}{2a}(X^2 - x^2) \hspace{2cm} \rho \; = \; g \frac{1 + \frac{X^2}{a^2}}{\left(1 + \frac{x^2}{a^2}\right)^2} \hspace{2cm} \mu \; \ge \; \frac{\frac{x}{a}\left(1 + \frac{X^2}{a^2}\right)}{\lambda\left(1 + \frac{x^2}{a^2}\right)^2 + 1 + \frac{X^2}{a^2}}$ Thus the particle will come to rest when $x=X$ , and this motion is possible provided that $\mu \; \ge \; \frac{\frac{x}{a}\left(1 + \frac{X^2}{a^2}\right)}{\lambda\left(1 + \frac{x^2}{a^2}\right)^2 + 1 + \frac{X^2}{a^2}} \hspace{1cm} 0 \le x \le X$ For ease, define $p = 1 + \tfrac{x^2}{a^2}$ and $P = 1 + \tfrac{X^2}{a^2}$ . Then we need $\mu \ge Q(p) \; = \; \frac{P\sqrt{p-1}}{\lambda p^2 + P} \hspace{1cm} 1 \le p \le P$ Note that $Q'(p) \; = \; \frac{\lambda P}{2\sqrt{p-1}(\lambda p^2 + P)^2}\big[P\lambda^{-1} + 4p - 3p^2\big] \; = \; \frac{\lambda P}{2\sqrt{p-1}(\lambda p^2 + P)^2}Z(p) \hspace{1cm} p > 1$ and $Z(p)$ is a decreasing function for $p > 1$ , with $Z(1) = P\lambda^{-1} + 1 > 0$ and $Z(P) = P(4 + \lambda^{-1} - 3P)$ . If $P < \tfrac13(4 + \lambda^{-1})$ then we deduce that $Q(p) \; \le \; Q(P) \; = \; \frac{\sqrt{P-1}}{\lambda P + 1} \hspace{1cm} 1 \le p \le P$ On the other hand, if $P > \tfrac13(4 + \lambda^{-1})$ , then $Z(\hat{p}) = 0$ , where $1 < \hat{p} = \tfrac13\left(2 + \sqrt{4 + 3P\lambda^{-1}}\right) < P$ , and hence $Q(p) \; \le \; Q(\hat{p}) \; = \; \frac{3P\sqrt{3}\sqrt{\sqrt{4 +3P\lambda^{-1}} - 1}}{8\lambda + 12P + 4\lambda\sqrt{4 + 3P\lambda^{-1}}} \hspace{1cm} 1 \le p \le P$ In summary, an initial speed $v$ will result a maximum horizontal displacement $X = v\sqrt{\tfrac{a}{g}}$ . If we define $P = 1 + \tfrac{X^2}{a^2} = 1 + \tfrac{v^2}{ag}$ , then this motion is possible provided that $\mu \ge H(P)$ where $H(P) \; = \; \left\{ \begin{array}{lll} \displaystyle\frac{\sqrt{P-1}}{\lambda P + 1} & \hspace{1cm} & P < \tfrac13(4 + \lambda^{-1}) \\[2ex] \displaystyle\frac{3P\sqrt{3}\sqrt{\sqrt{4 +3P\lambda^{-1}} - 1}}{8\lambda + 12P + 4\lambda\sqrt{4 + 3P\lambda^{-1}}} & & P > \tfrac13(4 +\lambda^{-1}) \end{array}\right.$ It is not hard to see that $H$ is a continuous increasing function of $P \ge 1$ , and that $H(P) \to \infty$ as $P \to \infty$ . Thus, for any value of $\mu$ , there is a unique value $\hat{P}$ such that $\mu = H(\hat{P})$ , and this means that the maximum initial speed that is possible is $v_{\mathrm{max}} = \sqrt{(\hat{P}-1)ag}$ .

We are told that $M > \tfrac12m$ , so that $\lambda > \tfrac12$ . This means that $4\lambda > \tfrac13(4 + \lambda^{-1})$ , and we can now calculate that $H(4\lambda) = \tfrac12$ . Thus, if $\mu = \tfrac12$ , we have $\hat{P} = 4\lambda$ , and hence the maximum possible initial speed of the particle is $v_{\mathrm{max}} \; = \; \sqrt{(4\lambda - 1)ag} \; = \; \sqrt{\frac{4M-m}{m}ag}$ which makes the answer $4 + 1 + 1 = \boxed{6}$ .