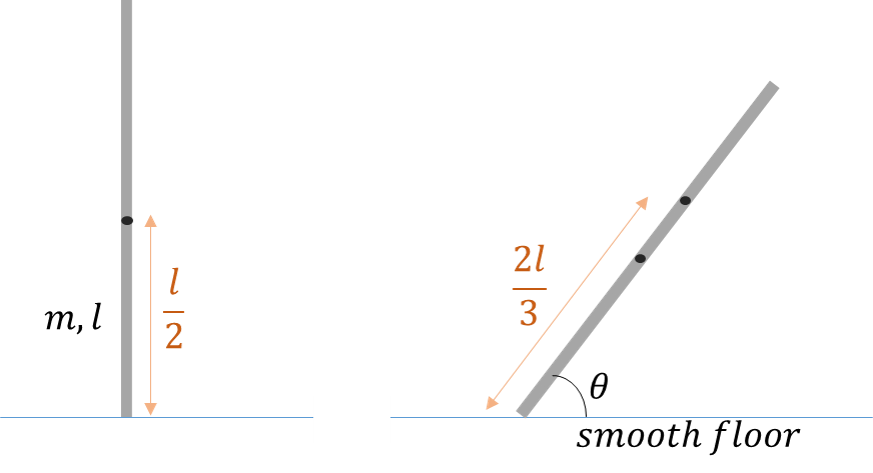
Sliding rod (I)

Since there is no friction, the center of mass will move vertically down. When the rod is horizontal, the center of the rod will be at the original support point, and the selected point will be at a distance of $\frac{1}{6} \ell$ from the original support point. Assuming that the orbit is really ellipse, we can see that the semi major axis is $a=\frac{2}{3} \ell$ (the original starting position of the selected point) and the semi minor axis is $b=\frac{1}{6} \ell$ . the eccentricity is $e=\sqrt{1-\frac{b^2}{a^2}}=0.968$ .

To see that the orbit is really an ellipse, look at https://en.wikipedia.org/wiki/Ellipse and scroll down to the "paper strip method".