Sliding rod (II)

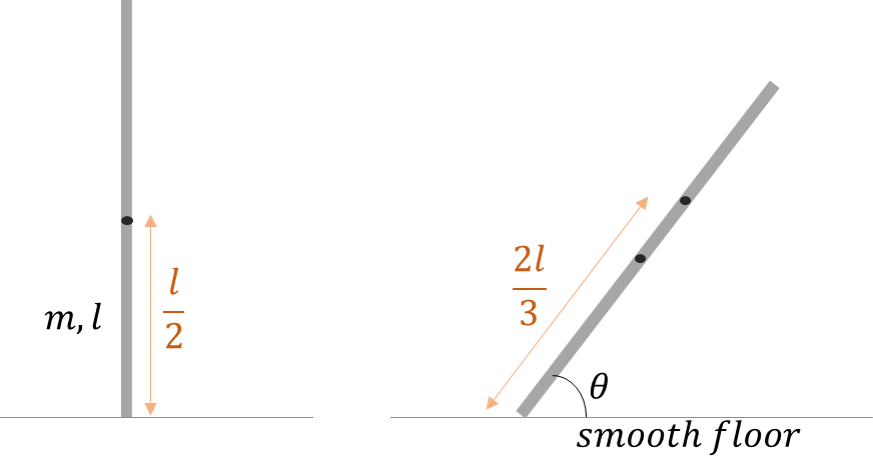
A thin rod of mass $m$ and length $l$ is kept vertically on a smooth table. It is given a slight push such that it starts moving due to uniform gravitational field $g$ present in vertically downwards direction. The acceleration of center of mass is given by ${ a }_{ cm }(\theta )\quad =\quad g\cdot \frac { a }{ { (b-a{ sin }^{ 2 }\theta ) }^{ c } } \left( d+esin\theta -f{ sin }^{ 2 }\theta +i{ sin }^{ 4 }\theta \right)$ where $a$ , $b$ , $c$ , $d$ , $e$ , $f$ and $i$ are positive integers. Find the value of $a+b+c+d+e+f+i$ .