Sliding Sine Window
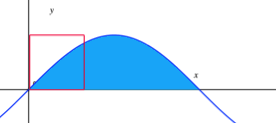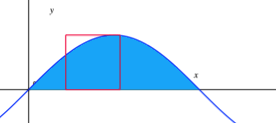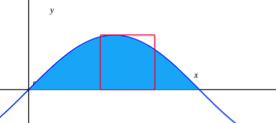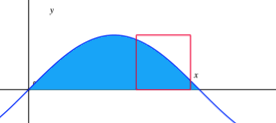
A square of side length one rests in the first quadrant with two of its sides sitting on the coordinate axes, overlapping the region between y = sin x and the x -axis. It then slides along the positive x -axis at a rate of 1 unit per second as shown above.
At what rate is the area inside both the blue region and the square changing after 1 second?
The answer is 0.0678.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Did the same way. A simple and elegant solution!
Same method sir!
Brian, I really look up to you. For the first time I can proudly say I aporoached a problem the same way you did :)
Log in to reply
That's great, Andrew, and I'm honored that you look up to me. :)
I thought of posting a similar problem with a rolling circle, (radius 1/2), rather than a sliding square, but that would have made for some messy calculations that would have relied too much on WolframAlpha.
Same strategy. ;) Solution (+1).
 A wave entering a
A wave entering a
If one were to take a more physical approach without calculus, imagine the square to be a pipe (with its axis parallel to the x-axis and a rectangular cross section) The sine function graph is a water wave entering it. The rate at which the blue region (water) inside the pipe changes is t i m e W a t e r F l o w i n g I n − W a t e r F l o w i n g O u t = d t sin ( 2 ) d x − sin ( 1 ) d x = [ sin 2 − sin 1 ] × d t d x = [ s i n 2 − s i n 1 ] × 1 = 0 . 0 6 7 8
Relevant wiki: Fundamental Theorem of Calculus
Letting x ( t ) be the position of the lower-left corner of the square at time t we have that x ( t ) = t . Since the square and the blue region both have a "ceiling" of 1 , the area A inside both the blue region and the square is just the area inside the blue region from t to t + 1 , i.e.,
A = ∫ t t + 1 sin ( θ ) d θ for t ∈ [ 0 , π − 1 ] .
We are looking for d t d A when t = 1 , and by the Fundamental Theorem of Calculus we have that
d t d A = sin ( t + 1 ) − sin ( t ) , which at t = 1 is sin ( 2 ) − sin ( 1 ) = 0 . 0 6 7 8 to 3 significant figures.