Sliding Up an Elliptical Loop
A massive point-particle is sliding on the inside of a smooth elliptical loop, described by the following equation (distances in meters): 9 x 2 + 4 y 2 = 1 . Initially, the particle is at ( x , y ) = ( 3 , 0 ) , and its velocity is upward and tangential to the curve. Gravity is 1 0 m/s 2 in the − y direction.
What is the minimum initial speed ( in m/s ) required for the particle to reach ( x , y ) = ( 0 , 2 ) without flying off of the loop on the way there?
The answer is 9.2195.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Sir, in the last and second last lines, it should be 2 v 2 ≥ 1 7 g instead of v 2 as derived by you in the preceding line.
9
x
2
+
4
y
2
=
1
Taking derivative,
9
2
x
d
x
+
4
2
y
d
y
=
0
d
x
d
y
=
−
9
y
4
x
⋯
(
⋆
)

At the highest point, for the particle,
m
g
+
N
by loop
=
m
d
t
d
v
.
For the particle to reach the top without losing contact with the loop with minimum initial velocity, at the highest point, the value of
N
should be just negligibly greater than
0
. So,
d
t
d
v
=
g
.
Here's how we can find acceleration at the point
(
0
,
2
)
:
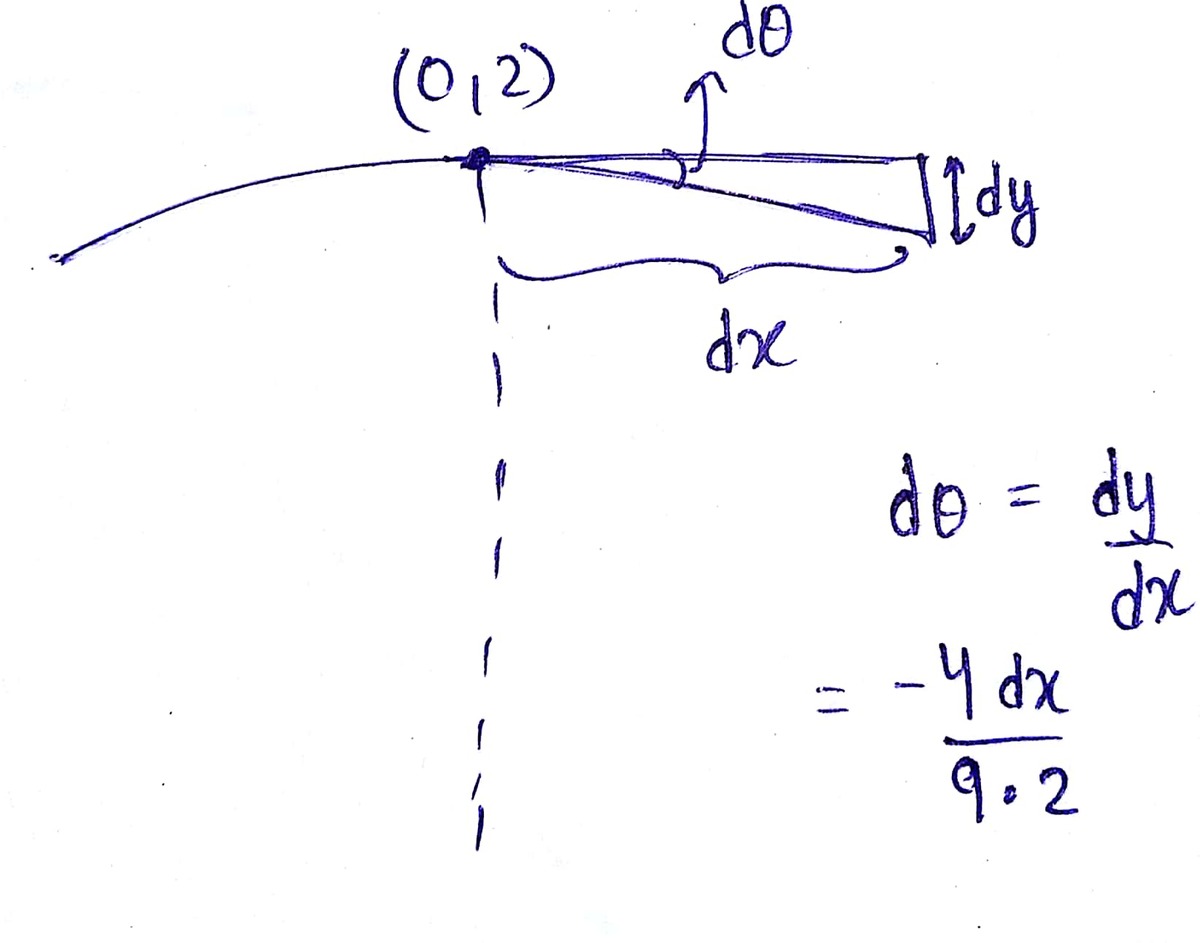 d
V
x
=
v
(
cos
d
θ
−
1
)
≈
0
,
d
V
y
=
v
sin
d
θ
≈
v
d
θ
So
d
t
d
v
=
v
d
t
d
θ
=
9
−
2
v
2
=
−
g
.
(Since
d
x
/
d
t
=
v
)
So
v
2
=
2
9
g
⟹
v
0
2
=
2
1
7
g
.
d
V
x
=
v
(
cos
d
θ
−
1
)
≈
0
,
d
V
y
=
v
sin
d
θ
≈
v
d
θ
So
d
t
d
v
=
v
d
t
d
θ
=
9
−
2
v
2
=
−
g
.
(Since
d
x
/
d
t
=
v
)
So
v
2
=
2
9
g
⟹
v
0
2
=
2
1
7
g
.
@Harsh Poonia can we do it without calculus With only work energy theorem
Log in to reply
You would need calculus to get the radius of curvature and acceleration.
The position, velocity and acceleration vectors of a particle touching the ellipse can be given by r = ( 2 sin θ 3 cos θ ) r ˙ = ( 2 cos θ − 3 sin θ ) θ ˙ r ¨ = ( 2 cos θ − 3 sin θ ) θ ¨ − ( 2 sin θ 3 cos θ ) θ ˙ 2 The normal reaction between the particle and the ellipse will be of the form R = − m λ ( 3 sin θ 2 cos θ ) where λ > 0 , and the equation of motion of the particle is m r ¨ = R + ( − m g 0 ) ( ⋆ ) Taking the scalar product of ( ⋆ ) with ( 2 cos θ − 3 sin θ ) , we obtain ( 9 sin 2 θ + 4 cos 2 θ ) θ ¨ + 5 sin θ cos θ θ ˙ 2 d θ d [ 2 1 ( 9 sin 2 θ + 4 cos 2 θ ) θ ˙ 2 + 2 g sin θ ] 2 1 ( 9 sin 2 θ + 4 cos 2 θ ) θ ˙ 2 + 2 g sin θ θ ˙ 2 = − 2 g cos θ = 0 = 2 1 v 2 = 4 + 5 sin 2 θ v 2 − 4 g sin θ Taking the scalar product of ( ⋆ ) with ( 3 sin θ 2 cos θ ) , we obtain that λ = 4 + 5 sin 2 θ 3 ( 2 θ ˙ 2 − g sin θ ) = ( 4 + 5 sin 2 θ ) 2 3 [ 2 v 2 − g sin θ ( 1 2 + 5 sin 2 θ ) ] and hence, to reach the top of the ellipse, we must have λ ≥ 0 throughout the motion, and so 2 v 2 ≥ g sin θ ( 1 2 + 5 sin 2 θ ) 0 ≤ θ ≤ 2 1 π The RHS of this inequality is an increasing function of θ , so we want 2 v 2 ≥ 1 7 g , and hence v ≥ 9 . 5 g = 9 . 2 1 9 5 4 4 4 5 7 m s − 1 .