Slipping Tipping Rod
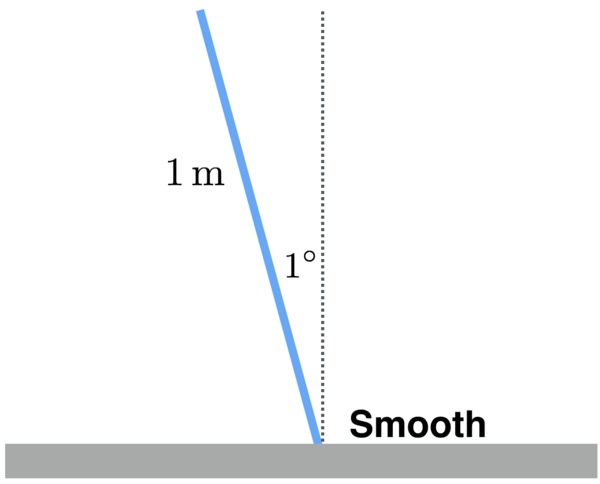
A massive, rigid, uniform rod is initially at rest, tilted one degree away from the vertical. The rod stands on a smooth surface, and its bottom end can slide along the surface.
How many seconds does it take for the rod to become horizontal?
Details and Assumptions:
- The rod is 1 meter long.
- There is a downward gravitational acceleration .
- While the bottom end of the rod can slide along the surface, it cannot lose contact with it.
The answer is 0.8034.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Problem solving 2D
Since all forces acting on the rod are vertical, the centre of mass of the rod does not move horizontally. Thus, if the rod has length a , and it makes an angle of θ with the vertical, then its centre of mass must be a height 2 1 a cos θ above the ground. Thus the rod has kinetic energy 2 1 m ( 2 1 a sin θ θ ˙ ) 2 + 2 1 × 1 2 1 m a 2 θ ˙ 2 = 2 4 1 m a 2 ( 1 + 3 sin 2 θ ) θ ˙ 2 and so conservation of energy tells us that 2 4 1 m a 2 ( 1 + 3 sin 2 θ ) θ ˙ 2 + 2 1 m g a cos θ = 2 1 m g a cos θ 0 where θ 0 = 1 ∘ is the initial inclination of the rod. Thus the time to reach the horizontal is T = ∫ θ 0 2 1 π 1 2 g ( cos θ 0 − cos θ ) a ( 1 + 3 sin 2 θ ) d θ = 0 . 8 0 3 3 8 8 s with a = 1 m and g = 1 0 m s − 2 .