Slipt checkboard

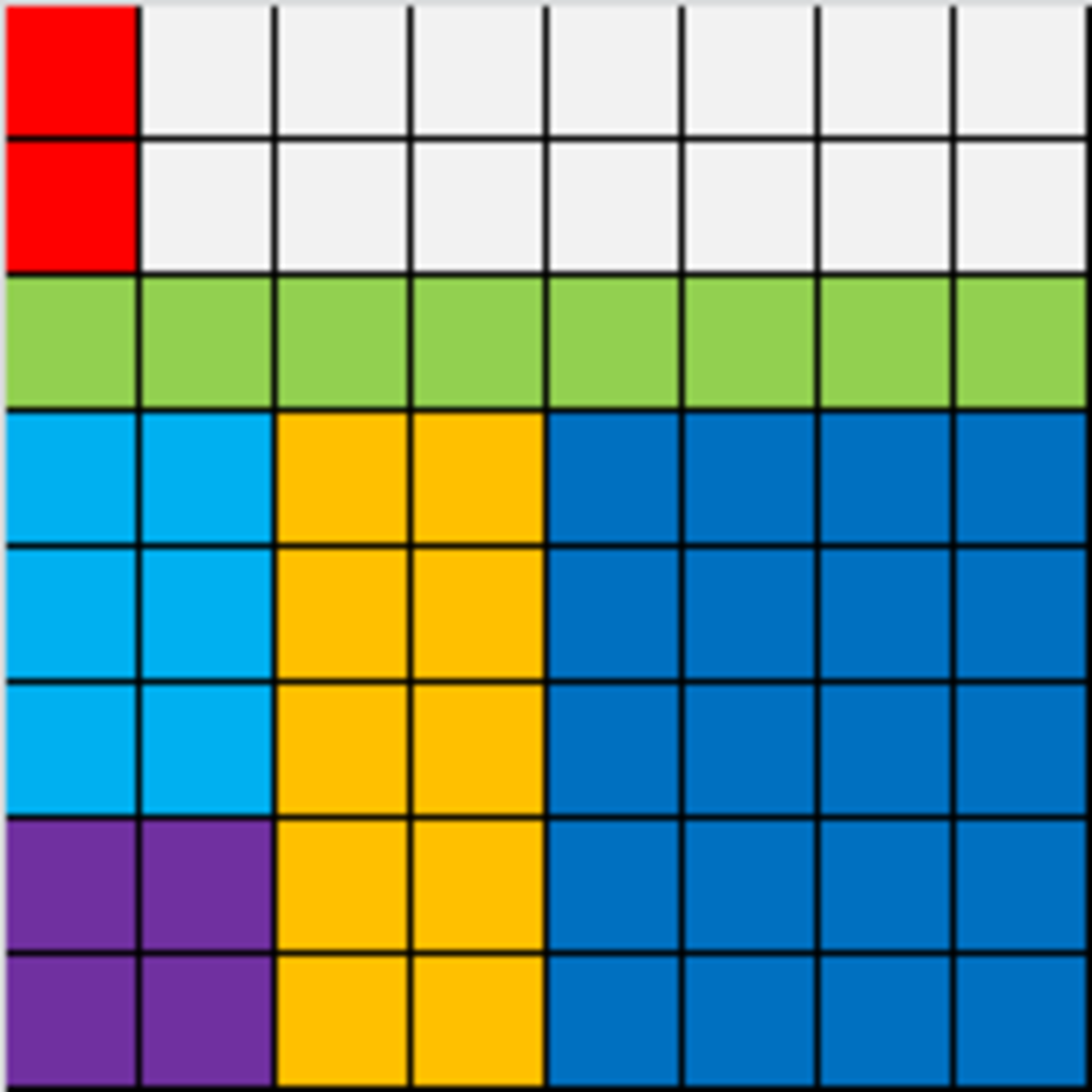
Assuming checkerboard is the standard 8x8 chessboard. (Checkers have two common sizes, 8x8 and 10x10.)

Condition 1 requires the rectangles to have an even area. On the other hand, any rectangle (along the gridlines) with even area will satisfy condition 1, so we can replace condition 1 with "each rectangle has an even area".

Suppose there are $n$ rectangles. The minimum area covered is $2+4+6+\ldots+2n = n(n+1)$ , due to condition 2 requiring all rectangles to have different areas. Thus we need $n(n+1) \le 64$ , or $n \le 7$ . So the theoretical maximum is $\boxed{7}$ rectangles. This is achievable in many ways; here's one that I think of:

We have that $32\geq 1+2+3+4...p=\frac{p(p+1)}{2}$ where $64\geq p(p+1)$ so $p\leq7$ .

$\therefore$ all the posible descomposition with $p=7$ are:

$1+2+3+4+5+6+11=32$ this is not possible by $11$

$1+2+3+4+5+7+10=32$

$1+2+3+4+5+8+9=32$

$1+2+3+4+6+7+9=32$

$1+2+3+5+6+9+8=32$

The last four can be form $\therefore$ the maximum $\boxed{p=7}$