Slumber Party
Claire is going to walk to her friend Katie's house to have a slumber party. Their neighborhood is arranged in a square grid such that Katie's house is exactly 6 lengths up, and 6 lengths right from Claire's house.
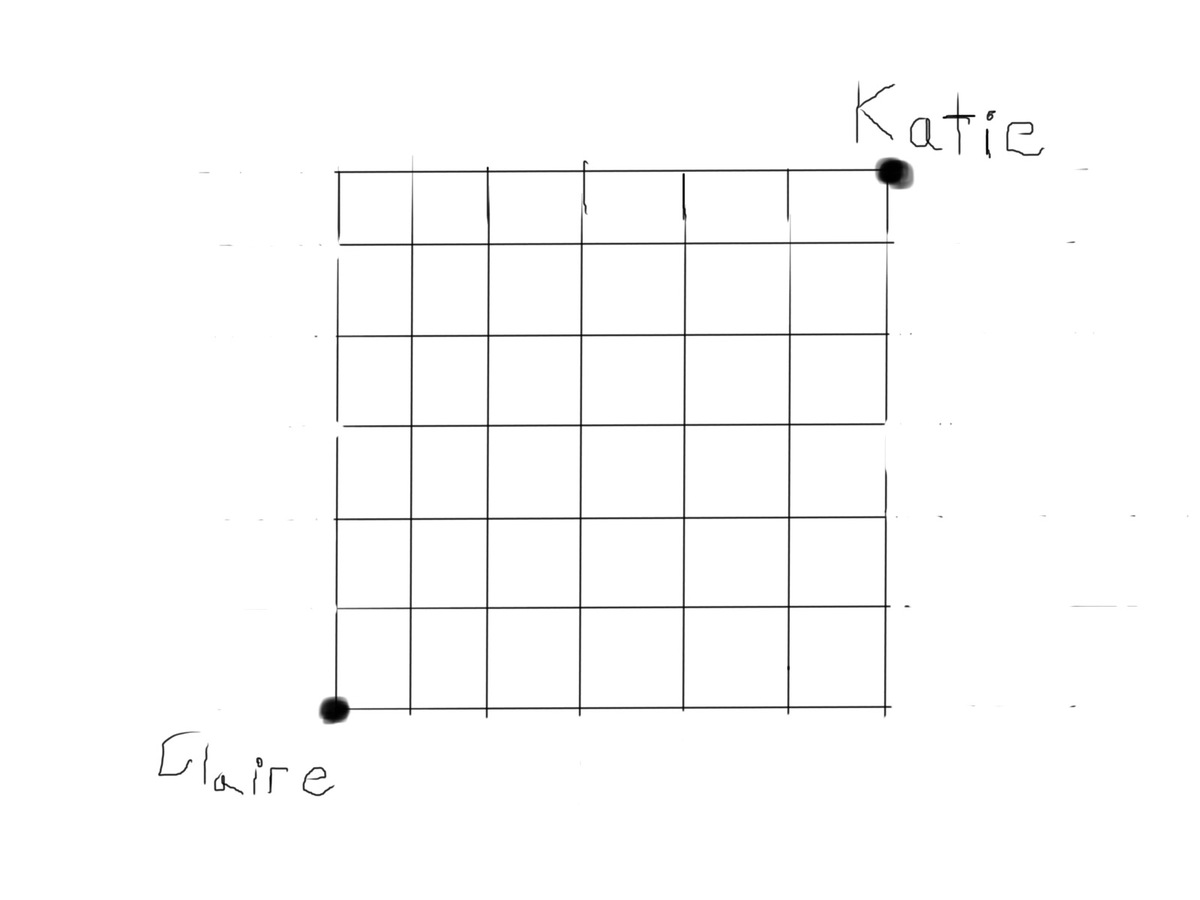
If Claire must travel along the lines, and will only move Up or to the right, and cannot move outside the 6X6 grid shown, how many different paths can she take to get to Katie's house?
The answer is 924.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
One way to look at this problem is to look at Claire's set of moves as an 12 character string consisting of 6 'R' characters, and 6 'U' characters (representing Right and Up respectively, the two directions she can travel)
To solve the number of possible arrangements that a word/string with repeating letter can have, the formula is
where each letter is distinct.
This simplifies to 6 ! ∗ 6 ! 1 2 ! which simplifies to [12 Choose 6] which is 924.