Sly Stormy Snowy Snowflake
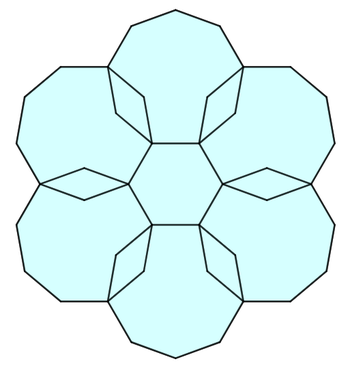
As shown above, the unit regular hexagon is surrounded by six unit regular nonagons. Altogether, they form the cyan polygon, having sides all of the unit length. Its area can be expressed as follows:
where are all nonnegative integers. Which of these four variables contain(s) the unique value?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The snowflake can be tiled with 6 unit rhombi with an interior angle of 9 π (purple), 1 8 unit rhombi with an interior angle of 9 2 π (light blue), 2 4 unit rhombi with an interior angle of 3 π (dark blue), and 1 2 unit rhombi with an interior angle of 9 4 π (green).
So one way the area can be expressed is 6 sin 9 π + 1 8 sin 9 2 π + 2 4 sin 3 π + 1 2 sin 9 4 π , where A = 1 , B = 3 , C = 4 , and D = 2 .
Knowing the total area, the Python computer program below can be used to brute force other possible non-negative integer values for A , B , C , and D . Out of all the possibilities, C only has a unique value of 2 4 .
(We can also observe that there are always solutions for B = A + 1 2 and D = 1 8 − A because of the identity sin 9 π + sin 9 2 π = sin 9 4 π .)