Conservation of Momentum

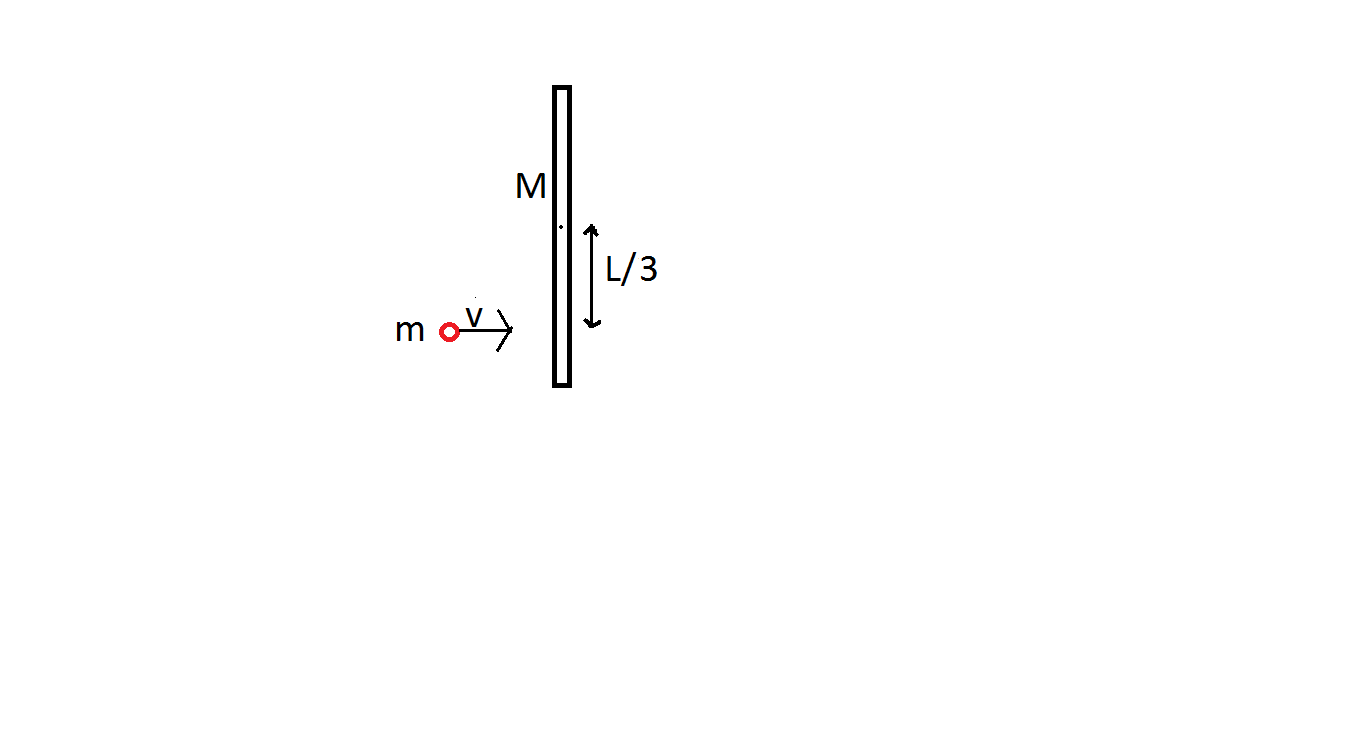
A small mass is thrown with a velocity of $\SI[per-mode=symbol]{2}{\meter\per\second}$ toward a rod, a distance of $\ell/3$ from its center. The rod is hinged at the centre.

You are given that the mass is $\SI{6}{\kilo\gram}$ , and its length $\ell = \SI{3}{\meter}$ and the mass of the small object is $\SI{3}{\kilo\gram}.$ Upon collision, the small mass sticks to the rod.

Find the angular velocity of the rod after this impact (in $\si[per-mode=symbol]{\radian\per\second}$ ).