Smaller hexagon in a Hexagon
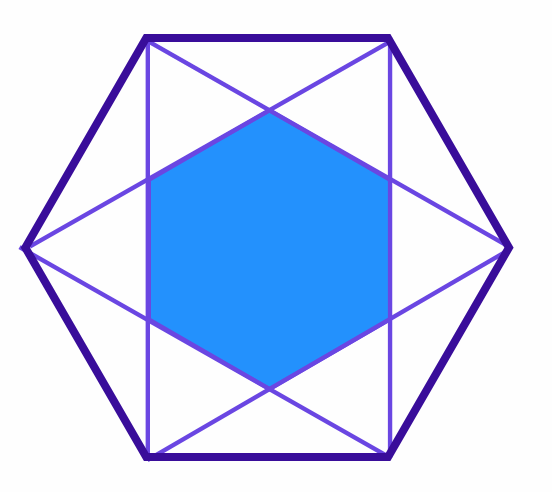
What is the ratio of the areas of the blue hexagon to the large hexagon?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions

@Mahdi Raza ,how do you make this animation
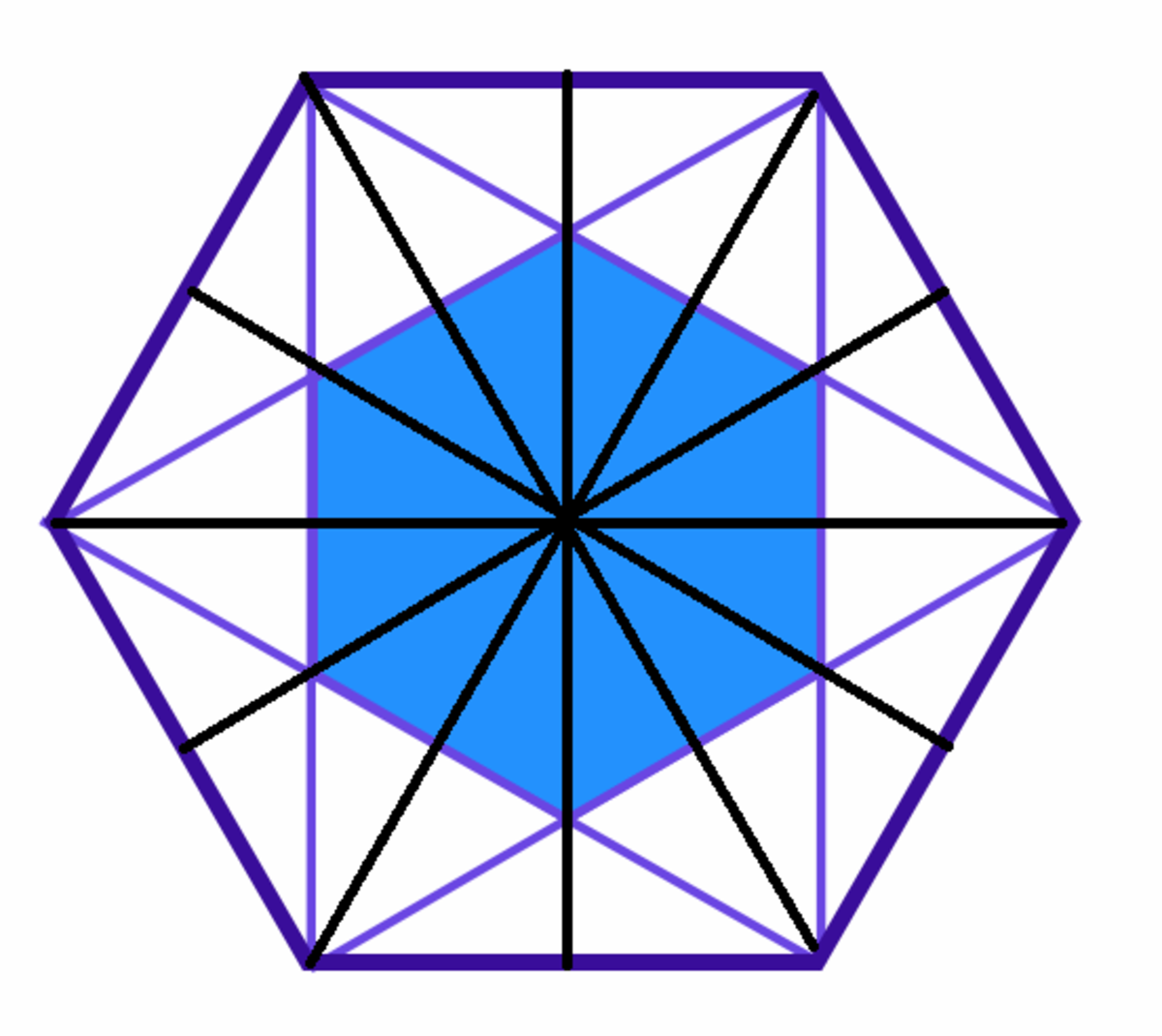
For each blue region, there are 2 corresponding white regions of same area. Hence 3 1 .
Nice, thank you for sharing!!
Log in to reply
https://brilliant.org/problems/a-solid-problem/ ...visit my nem problem
Each side of the smaller hexagon is of length b = 3 a , where a is the length of each side of the bigger hexagon. Hence the required ratio is ( a b ) 2 = 3 1 .
Great, thank you for sharing!!
@Alak Bhattacharya , where did you get √ 3 from? I have no idea where you got that from.
Log in to reply
Look at the diagram given in the problem. As I have defined the lengths, b + b + b = 2 a sin ( 2 1 2 0 ° ) = a 3 ⟹ b = 3 a
a
r
(
A
B
C
)
=
a
r
(
A
B
D
)
smaller hexagon= 6 a r ( A B C )
Larger hexagon = 1 8 a r ( A B C )
So,ratio = 3 1
It is clear to see that the hexagon can be divided to six triangles, and that the sum of the triangles are equal to the sum of the angles in contact with the hexagon.
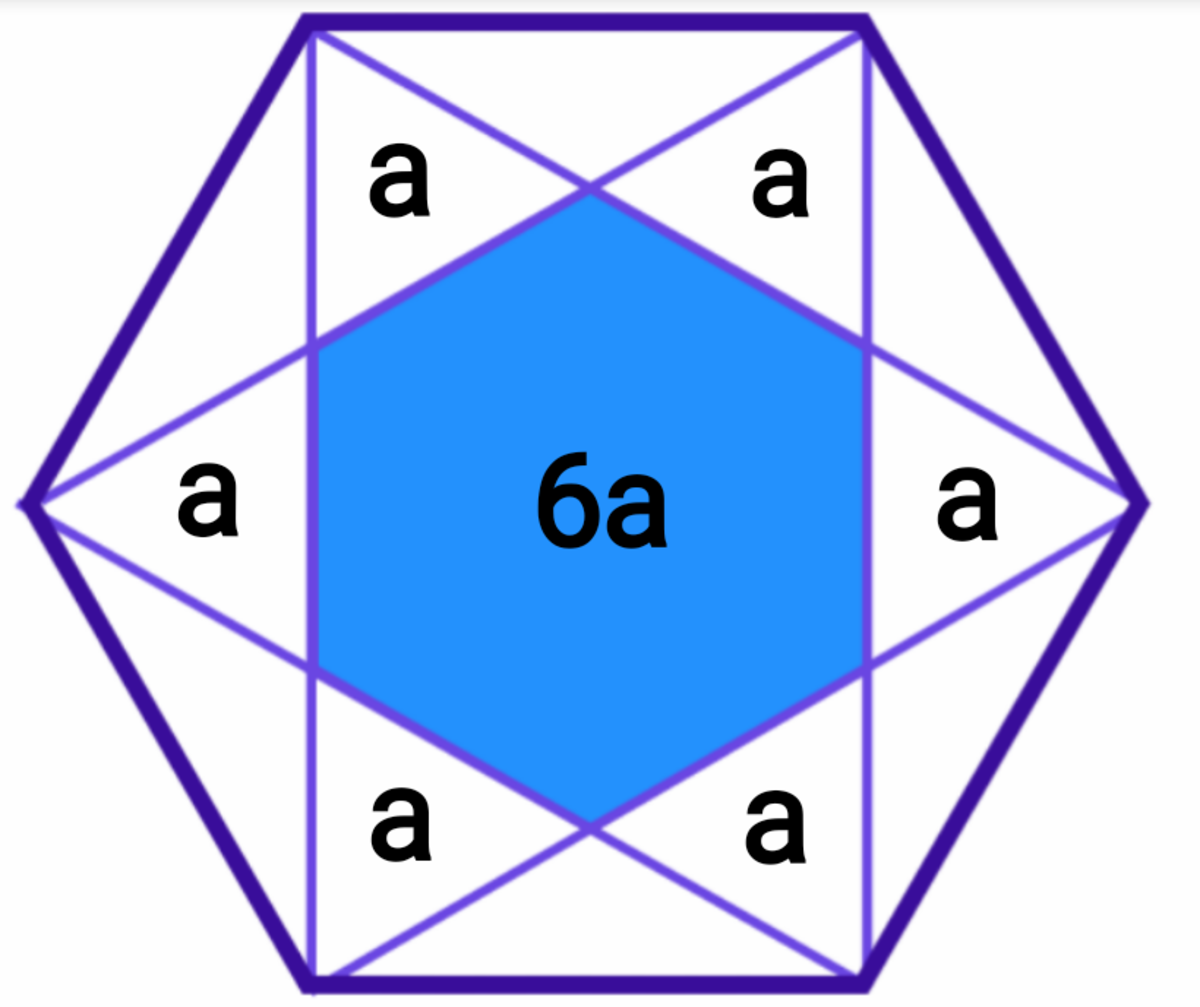
We can also notice that the triangles on contact with the large hexagon, when split to two, can rearrange and form a triangle similar to the one found above.
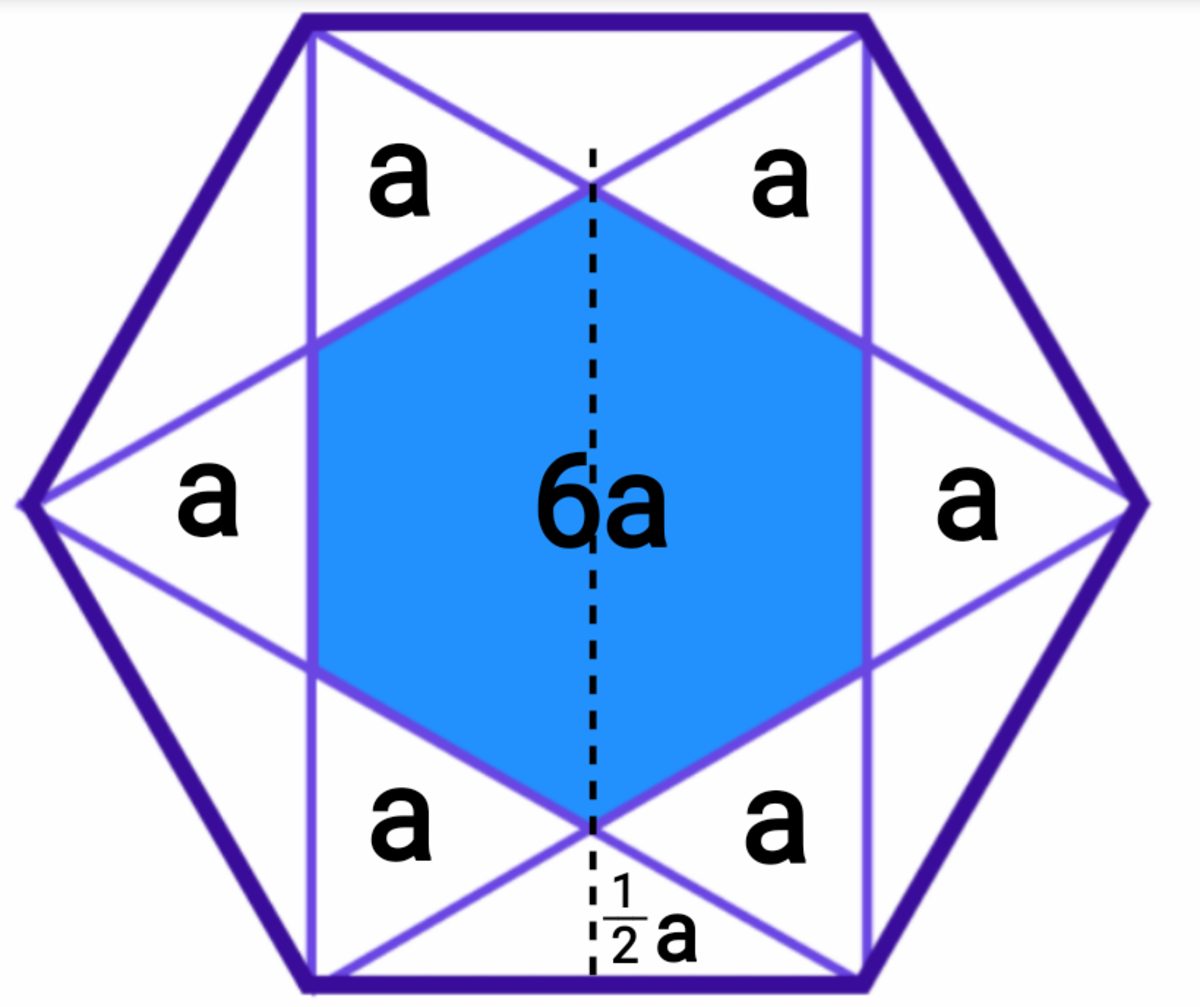
Therefore, as we can create three figures with the same area, and only the smaller hexagon is shaded blue, only 3 1 of the large hexagon is shaded blue.
Great, thank you for sharing!!