Smallest Equilateral Triangle
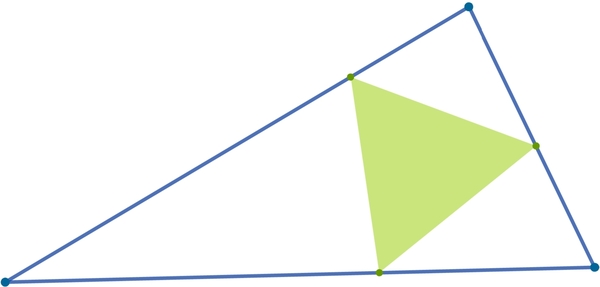 An equilateral triangle is drawn such that its vertices lie on the different sides of a
.
An equilateral triangle is drawn such that its vertices lie on the different sides of a
.
Find the ratio of the area of to the minimum possible area of the equilateral triangle.
For , and , the answer is , for positive coprime integers . Submit .
The answer is 32.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I was able to get the result with the help of a powerful solver, but i'm still curious to see an easier path.
I will just explain my overall approach:
With 3 angles provided in the question we can create the blue triangle with a base of any size. I think 1 is a good choice. We follow by creating 2 points that can only move on their respective sides. R and Q as an example. From those we create a line, and then a perpendicular to that line that passes through the middle point between R and Q. The intersection of that line with the base, will create a point S that is dependent on the other two points.
After that by setting a distance formula equating RQ and RS, this will turn the whole structure dependent on just one point which then can be used to minimize the equilateral.
The intersection of that line with the base, will create a point S that is dependent on the other two points.
After that by setting a distance formula equating RQ and RS, this will turn the whole structure dependent on just one point which then can be used to minimize the equilateral.
The final ratio is 3 6 + 2 2 1
The geometry is straight foward but algebraically it is a mess. The slopes given by tan θ don't seem to be the source of the square root form. There has to be a big simplification somewhere and hope someone points to it.