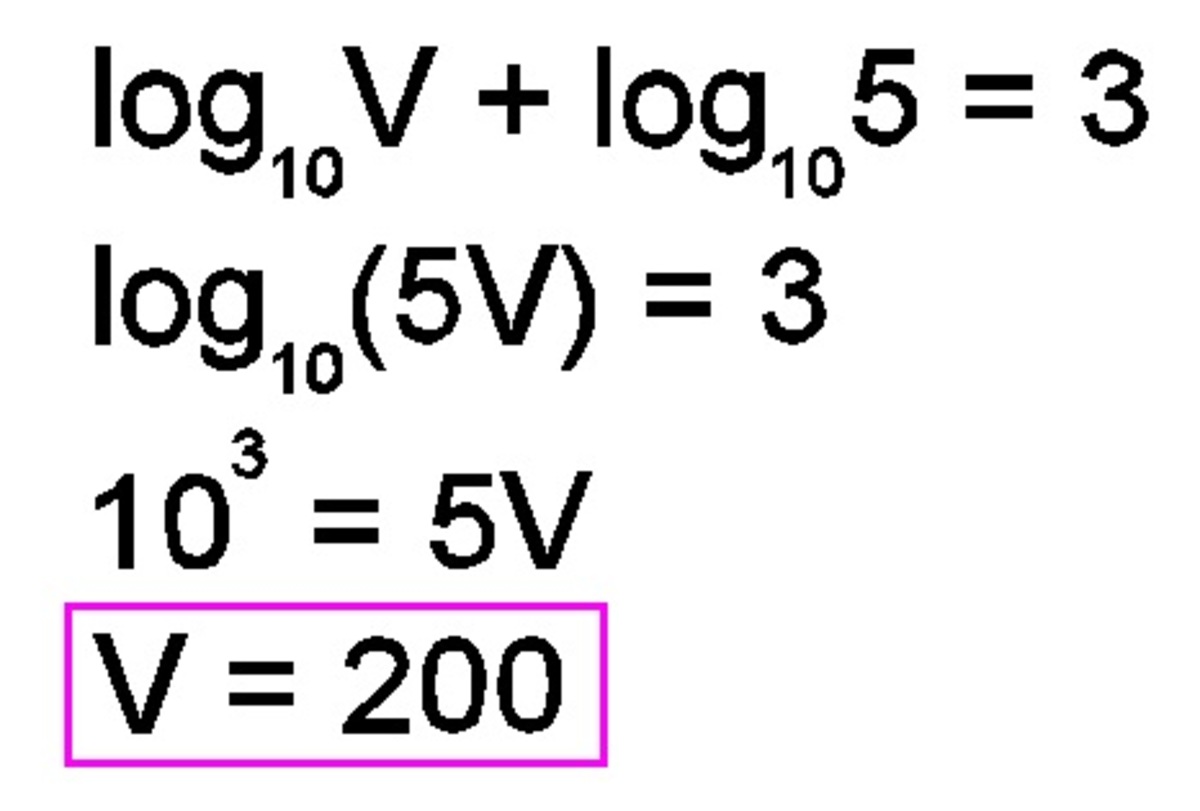Unknown Problem

Look at the given equation:

1.log v+log 5=3 Use the Product Property to combine the logarithms. log 5 v=3 Rewrite this as an exponential equation and solve for v.

2.log 5 v = 3 5 v = 103 5 v = 1,000 v = 200 Divide both sides by 5

3.The solution is valid only if the original equation makes sense when v is 200. In other words, the expression inside the logarithm in the original equation must be positive. log v+log 5 = 3 log 200+log 5 = 3 Plug in the solution, v=200 The expressions inside the logarithms are 5 and 200, which are positive. This means the logarithms in the original equation are well defined. So, v=200 is a valid solution.

$\log_{10}v + \log_{10}5$ = 1+1+1

$\log_{10}v + \log_{10}5$ = $\log_{10}10 + \log_{10}10 + \log_{10}10$ (since $\log_{10}10$ = 1)

$\log_{10}(5v) = \log_{10}1000$ (since log a + log b = log (ab) )

5v =1000

v=200