Smooth Slides
Two small, smooth slides lie within the same vertical plane, making the same angle α with the horizontal, as shown in the diagram. At some moment, the two small balls A and B are released simultaneously and they start sliding down. It took times t 1 and t 2 , respectively, for A and B to reach the ground.
At what time was the distance between the two balls the smallest?
Details and Assumptions:
- If your answer is of the form n t 1 2 − t 2 2 , where n is an integer, find n .
- Acceleration due to gravity is g .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let's find an easier way to look at this problem,
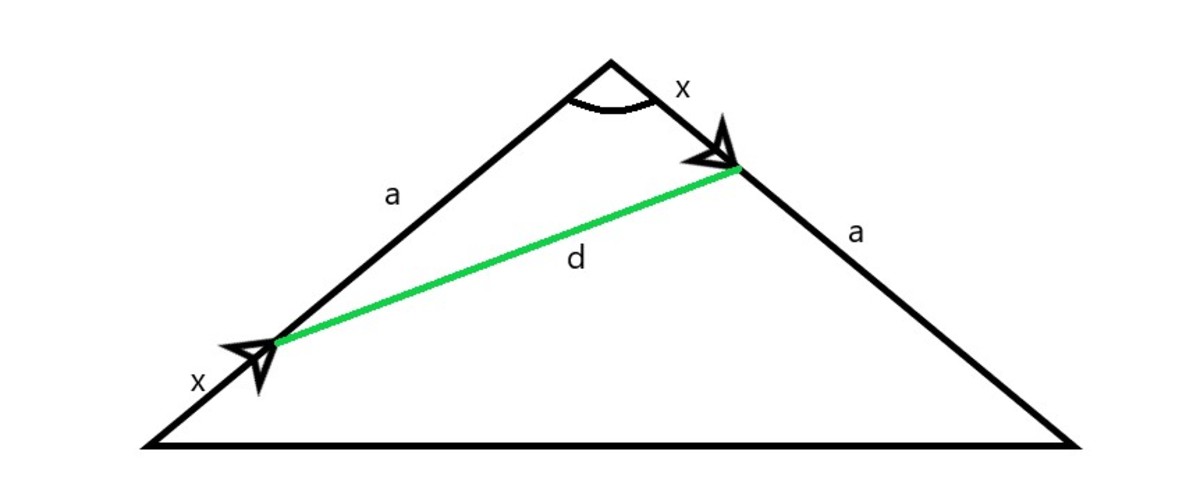
In this isosceles triangle, the only angle denoted θ , the isosceles side is a , x is variable which moving between 0 ≤ x ≤ a .
So we want to find minimum of d .
d 2 = x 2 + ( a − x ) 2 − 2 x ( a − x ) c o s θ
Take one derivative, to reach extreme value: d x d ( d 2 ) = 2 x − 2 ( a − x ) − 2 ( a − 2 x ) c o s θ = 0 .
Solving this, obtain x = 2 a
Using this property, we know that when ball A and ball B are align vertically, they will be in the shortest distance state.
let the length of longer slide be l 1 and shorter slide is l 2
So balls travel exactly 2 l 1 − l 2 and reach minimum distance.
After verify this fact, it is not hard to calculate that the time interval is 2 t 1 2 − t 2 2 .
n = 2 .
Excellent method using calculus!
First, consider the vertical motion of the two balls. They undergo the same vertical acceleration a y = g sin 2 α . Therefore their vertical distance remains constant. The distance between the balls is therefore smallest if their horizontal distance is smallest, i.e. zero.
Next, the horizontal motion of the balls is acceleration at rate a x = ± g sin α cos α . Therefore the horizontal motions are mirror images in a vertical line. The horizontal distance is zero at the line of reflection, which lies precisely between the initial position of the balls.
Now the horizontal component of the ramp length is proportional to the square of the time. Using symmetric coordinates, if ball B slides from x = 0 to x = − L B then ball A slides from x = − ( L A − L B ) to x = + L B . Thus the balls meet at position x = − 2 1 ( L A − L B ) . This means that t 2 = 2 1 ( t 1 2 − t 2 2 ) , or t = 2 1 ( t 1 2 − t 2 2 ) .