An ancient geometry problem
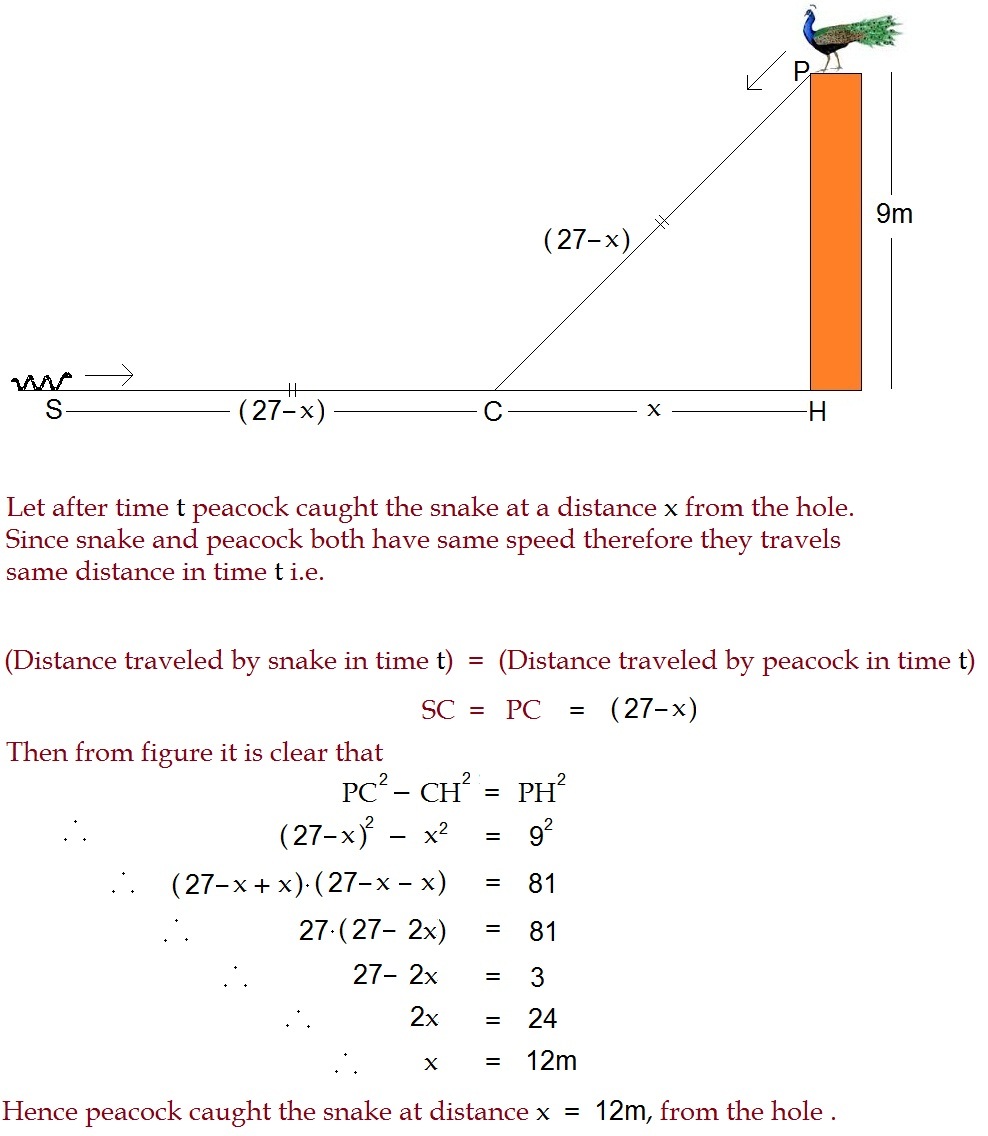
 A peacock is sitting on the top of a pillar which is 9m high. From a distance of 27m, a snake is coming to its hole at the bottom of the pillar. Seeing the snake, the peacock pounced upon it. If their speeds are equal then at what distance from the hole is the snake caught ?
A peacock is sitting on the top of a pillar which is 9m high. From a distance of 27m, a snake is coming to its hole at the bottom of the pillar. Seeing the snake, the peacock pounced upon it. If their speeds are equal then at what distance from the hole is the snake caught ?
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Let x be the the length that the peacock has to travel. Now using pythagoras' theorem, the length of the distance from the hole (where the snake and peacock will meet) = s q r t x 2 − 8 1 . This gives : x = 2 7 − x 2 − 8 1 ⇒ x 2 − 8 1 = 2 7 − x x 2 − 8 1 = 7 2 9 − 5 4 x ⇒ 5 4 x = 7 2 9 + 8 1 = 2 7 ( 2 7 + 3 ) = 2 7 × 3 0 x = 5 4 2 7 × 3 0 = 1 5 ∴ x 2 − 8 1 = 2 2 5 − 8 1 = 1 4 4 = 1 2
This problem is from the 12 century Indian math text Lilavati written by Bhaskaracharya or Bhaskara II. Here is an animated solution I posted long back.
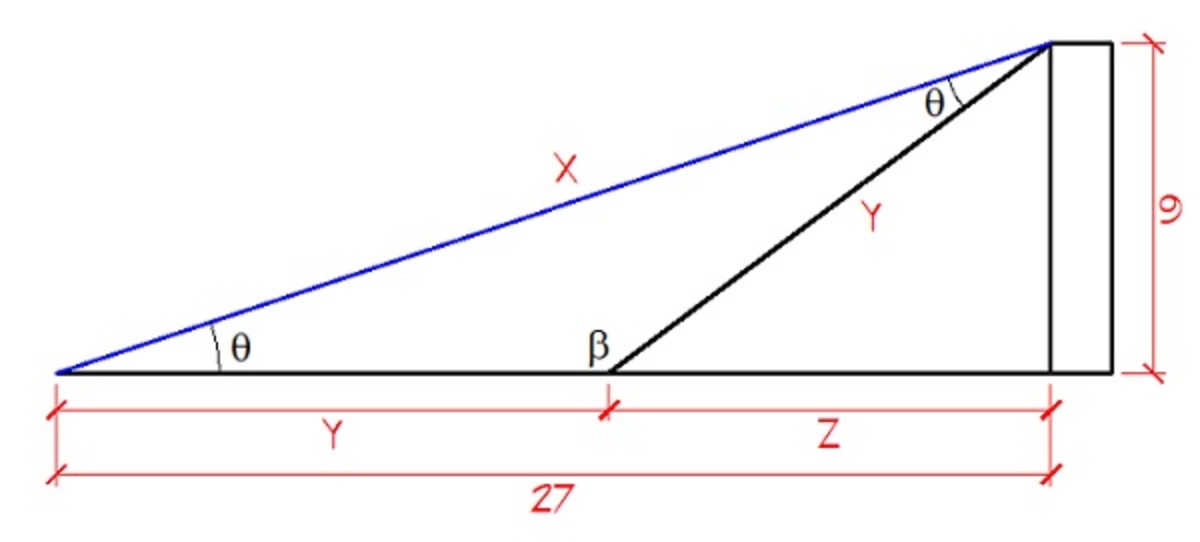
tan θ = 2 7 9 ⟹ θ = tan − 1 ( 2 7 9 ) ≈ 1 8 . 4 3 5
β = 1 8 0 − 2 ( 1 8 . 4 3 5 ) ≈ 1 4 3 . 1 3
By pythagorean theorem,
x = 2 7 2 + 9 2 = 8 1 0
By cosine law,
( 8 1 0 ) 2 = y 2 + y 2 − 2 ( y ) ( y ) ( cos 1 4 3 . 1 3 ) ⟹ y = 1 5
Finally,
z = 2 7 − 1 5 = 1 2