Snowman sniper
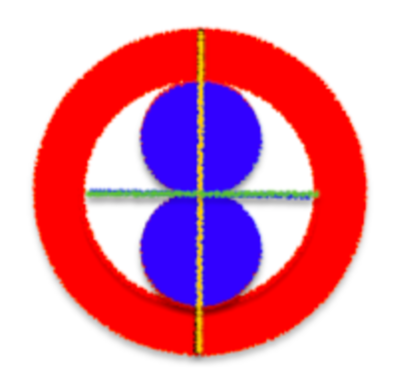 A sniper aims at a blue snowman. The snowman is fitted perfectly between the sniper's scope. The snowman is made of two identical circles (spheres in 3-D). If the ratio of the yellow line to the green line is
4
:
3
, what is the ratio the area of the snowman to the area of the scope (red area)?
A sniper aims at a blue snowman. The snowman is fitted perfectly between the sniper's scope. The snowman is made of two identical circles (spheres in 3-D). If the ratio of the yellow line to the green line is
4
:
3
, what is the ratio the area of the snowman to the area of the scope (red area)?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the radius of each of the blue circles be r and the distance from the point of intersection of the two lines to the edge of the figure be R .
We know that 4 r 2 R = 3 4 ⇒ 3 8 r = R .
∴ red blue = π ( 9 6 4 r 2 − ( 2 r ) 2 ) 2 π r 2 = 1 4 9
The area of a circle is πr^2.
we want to have an integer to multiply, so we could calculate easily.
Given that the snowman is fitted perfect between the scope, we could know that there is no gap between the scope and the snowman. Also, the snowman is made up of 2 identical circles, which means that their diameters are identical.
If we want an integer for the radiant for one of the circles in the snowman, we want the measurement of the green line to be a number that is still and integer even after we multiply it by 2^-2. the smallest number available is 4.
However, we also want it to be a multiple of 3, so that we could set a integer value for the measurement of the yellow line. The LCM of 3 and 4 is 12.
Given that the measurement of the yellow line is 12, the radiant of a blue circle 3, because 12*2^-2 = 3.
The area would be 9π since π3^2 is 9π.
Since there are 2 circles, we multiply it by 2, so the area of the snowman is 18π.
The measure meant of the yellow line will be 16 because the green line is 12 and the ratio of the yellow line and the green line is 4:3. ((12/3)*4=16)
if we find the area of the entire scope, we will have 8^2π, which is 64π. if we subtract the area of the lenses, which is 6^2π, or 36π, we will have 64π-36π, which is 28π. *The ratio for 18π to 28π is 9:14 *