Snuggle Up

Geometry Level 4

There are two circles , one with center A A and radius 1, the other with center B B and radius 2. The distance A B AB is 6. A third circle of unknown radius is tangent to both of these circles and there exists a straight line which

(1) is tangent to all three circles, and
(2) intersects the segment A B AB .

Find the radius of the third circle.

There are two solutions, R R and r r . Evaluate R − r R - r .


The answer is 3.375.

Marta Reece by Marta Reece , 69, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Marta Reece
May 20, 2016

The triangles DAC and DBE are similar, the latter being twice as large, therefore D will be twice as far from B as from A, giving us the distance DB as 4. Using the right triangle DBE we see that the angle DBE is 6 0 0 60^{0} (cosine equal to 1/2). The angle DAC is likewise 6 0 0 60^{0} . Now let's draw in the two large circles with radii R R and 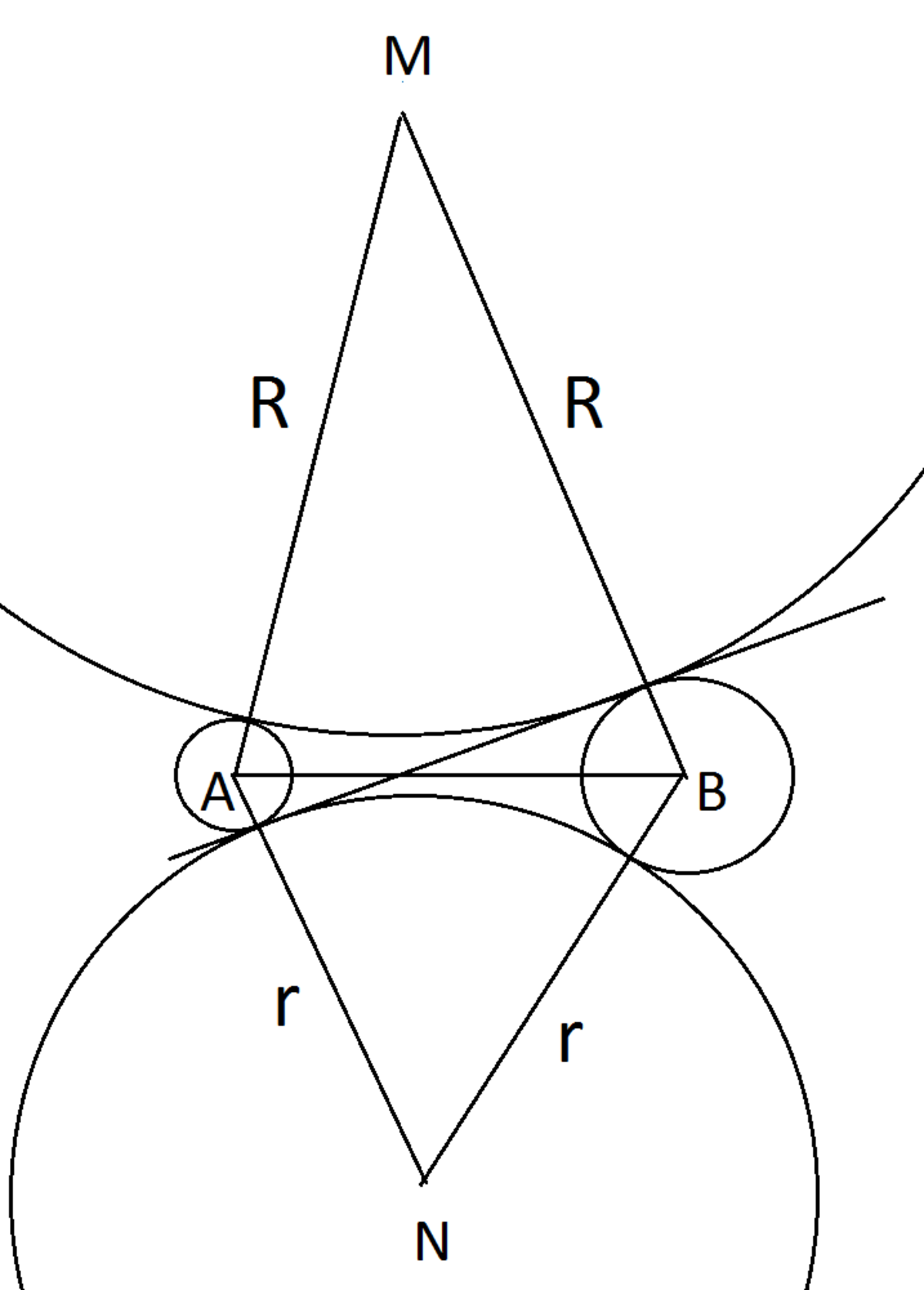r r .

Triangle ABM has sides R + 1 R+1 opposite the 6 0 0 60^{0} angle, 6 6 and R + 2 R+2 next to it. Law of cosines will give us

( R + 1 ) 2 = 6 2 + ( R + 2 ) 2 − 2 × 6 ( R + 2 ) × c o s ( 6 0 0 ) (R+1)^{2}=6^{2}+(R+2)^{2}-2\times6(R+2)\times cos(60^{0})

Solving for R R we get

R = 27 4 R=\frac{27}{4}

Triangle ABN has sides R + 2 R+2 opposite the 6 0 0 60^{0} angle, 6 6 and R + 1 R+1 next to it. Law of cosines will give us

( R + 2 ) 2 = 6 2 + ( R + 1 ) 2 − 2 × 6 ( R + 1 ) × c o s ( 6 0 0 ) (R+2)^{2}=6^{2}+(R+1)^{2}-2\times6(R+1)\times cos(60^{0})

Solving for R R we get

R = 27 8 R=\frac{27}{8}

Difference R − r = 27 8 = 3.375 R-r=\frac{27}{8} = 3.375 .

3 Helpful 0 Interesting 0 Brilliant 0 Confused

Please do not let your notation do double duty. I am currently unable to distinguish between your capital R and your small R. Can you edit your solution accordingly?

Calvin Lin Staff - 5 years ago

0 Helpful 0 Interesting 0 Brilliant 0 Confused

I believe that this is a solution to a different problem.

Marta Reece - 5 years ago

Log in to reply

So sorry. Thank you. I am correcting.

Niranjan Khanderia - 5 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...