So cute and yummy!
Compute
∫ − 1 1 1 − x 1 + x d x .
Give your answer to 3 decimal places.
The answer is 3.142.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
A simpler way is to split the integral into two: one from -1 to 0, the other from 0 to 1. Then use the substitution x → − x on one of the integrals. So you just need to evaluate ∫ 0 1 1 − x 2 2 d x , which is equal to π .
How can i learn calculus from basics to advance in a easy way
Log in to reply
You could try working through the calculus wikis on this site. I don't think that there is an "easy" way of learning calculus; there is a lot to learn and it requires plenty of practice. :)
rs agarwal
Pi, yummy and cute haha.
A slick but admittedly contrived method of solving the problem:
Note that ∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x when your function is Riemann Integrable.
So I = ∫ − 1 1 1 − x 1 + x d x = ∫ − 1 1 1 + x 1 − x
Then, 2 I = ∫ − 1 1 1 − x 1 + x + 1 + x 1 − x d x = ∫ − 1 1 1 − x 2 2 d x = 2 ( arcsin 1 − arcsin − 1 ) = 2 π
Thus I = π
Another way to solve this integral is replacing x by cos θ , which lead us to:
∫ − 1 1 1 − x 1 + x d x = ∫ π 0 1 − cos θ 1 + cos θ ( − sin θ ) d θ = ∫ 0 π tan ( 2 θ ) 1 2 sin ( 2 θ ) cos ( 2 θ ) d θ = 2 ∫ 0 π c o s 2 ( 2 θ ) d θ = 2 2 π = π
Note: tan 2 ( 2 θ ) = 1 + cos θ 1 − cos θ
I didn't know Euler substitution works as well! +1
Log in to reply
Sorry,some teachers complain about this way of solving this kind of problems, however it "always" works. My last step is integrating for parts, although there can be a lot ways to name it,it depends on the country,on the teachers and others factors, but it doesn't matter me.Thank you for upvoting me.
Log in to reply
Haha no problem. It's usually a last resort for me to apply Euler substitution, but yeah it simplifies the integrand tremendously.
Another Solution:
put x= sin theta
dx becomes cos theta dtheta
The limits for theta become -pi/2 to pi/2
The integrand has sqrt(1+sin theta)/sqrt(1-sin theta).
Use the identity (sin theta/2 + cos theta/2)^2=1+sin theta and (cos theta/2-sin theta/2)^2=1-sin theta
Then multiply and divide by cos theta/2+sin theta/2.
This will change the new integrand to 1+sin theta d theta within the limits -pi/2 to pi/2
Since sin theta is an odd function, this will simplify to integral -pi/2 to pi/2 d theta=pi
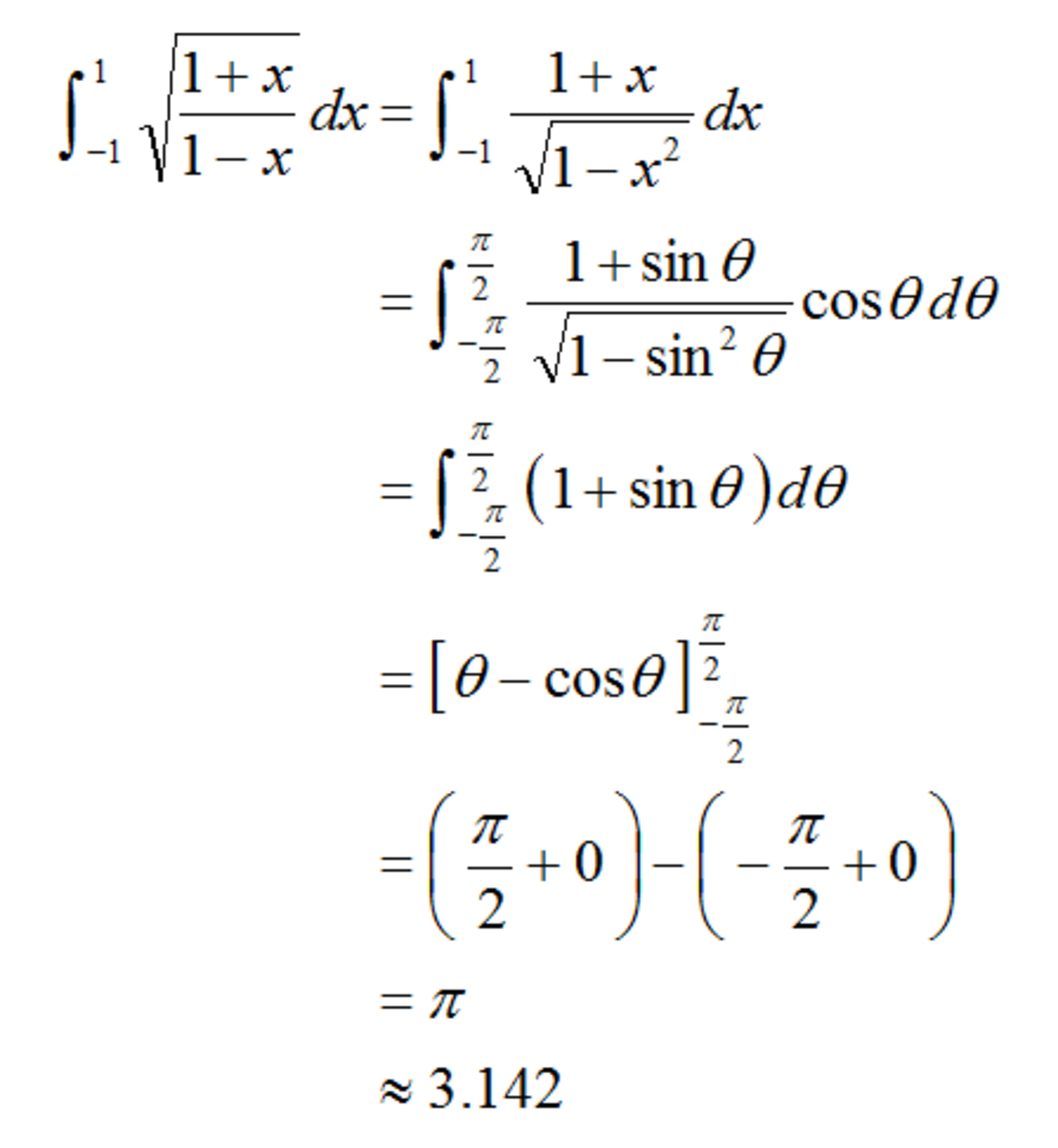
Note first that this is an improper integral (at the upper limit), so for now we will just deal with the indefinite integral and handle the limits at the end.
Multiply both the numerator and denominator of the integrand by 1 + x . The (indefinite) integral then becomes
∫ 1 − x 2 1 + x d x = ∫ 1 − x 2 1 d x + ∫ 1 − x 2 x d x .
For the first of these integrals let x = sin ( θ ) . Then d x = cos ( θ ) d θ and we just end up with
∫ 1 − sin 2 ( θ ) cos ( θ ) d θ = θ = sin − 1 ( x ) ,
(where I've ignored the constant of integration as we will make this integral definite in the last step).
For the second integral we use the substitution u = 1 − x 2 . Then d u = − 2 x d x , and the integral then becomes
− 2 1 ∫ u d u = − u = − 1 − x 2 .
So now bringing in the limits, our original integral comes out to
( sin − 1 ( x ) − 1 − x 2 ) ∣ − 1 1 = sin − 1 ( 1 ) − sin − 1 ( − 1 ) = 2 sin − 1 ( 1 ) = 2 ∗ 2 π = π = 3 . 1 4 1 5 9 2 6
to 7 decimal places.