One, Three, Nine, Twenty Seven

This is sum to infinity. $S_\infty$ = $\frac{a}{1-r}$

$S_\infty$ = $\frac{1}{1-\frac{1}{3}}$

$S_\infty$ = $1$ divided by $\frac{2}{3}$

$S_\infty$ = $\frac{3}{2}$

$S_\infty$ = $1.5$

Let the expression equals to $\Large x$

$\Large x=1+\frac13+\frac19+\frac{1}{27}+\ldots$

$\Large x=1+\frac13+\frac{1}{3\times3}+\frac{1}{3\times9}+\ldots$

$\Large x=1+\frac13\times\underbrace{(1+\frac13+\frac19+\frac{1}{27}+\ldots)}_x$

$\Large x=1+\frac13\times x$

$\Large x-1=\frac x3$

$\Large 3(x-1)=x$

$\Large \boxed{\boxed{x=\frac32}}$

Thinking of it in Base-three, each place value is a power of three.

It becomes 1 + .1 + .01 + .001 +... = 1.11111111111...

Then similar to Muhammad Ardivan's solution:

Let x = 1.11111111111... and   10x = 11.11111111111...
(Remember we're in base-three where you write three as 10 
and just shift the decimal point once to the right when you 
multiply by three.)

 10x = 11.11111111111...
- 1x =  1.11111111111...
so on the left: 
10x - 1x  (three x minus one x) = 2x

and on the right:
11.11111111111...
-1.11111111111...
======================
10.00000000000...

So 2x = 10  (three)

Divide both sides by 2
x = half of three =    1½

The sum of geometric progression with infinitely many terms is given by

$\boxed{S=\dfrac{a_1}{1-r}}$ where $a_1$ = first term and $r$ = common ratio

From the given geometric progression,

$r=\dfrac{1}{27} \div \dfrac{1}{9}=\dfrac{1}{9} \div \dfrac{1}{3}=\dfrac{1}{3} \div 1=\dfrac{1}{3}$

So the sum of the progression is,

$S=\dfrac{1}{\frac{1}{3}}=\dfrac{3}{2}=$ $\large \boxed{1.5}$

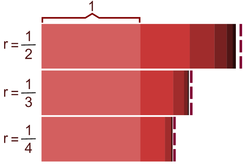
The image above shows the solution. The red bars depict the sums of 3 different infinite series by representing each consecutive fraction in the series as a shaded region with a length as a fraction of the first region. r=1/2 bar has a total length of 2. The length of the r=1/3 bar, when measured against the bar above, measures 1.5. So once you discover that r is 1/3 you can use the image to determine the length of the bar.
Alternatively (and this is what I did), you can just recall that the sum of an infinite series is the first term divided by 1-r, and you get 1/(1-(1/3)) = 1(2/3) = (3/2) = 1.5

Similar to @samuel ayinde

$\frac{a}{1-r}=\frac{1}{1-\frac{1}{3}}=\frac{3}{2}=\boxed{\large{1.5}}$

I bet that my method is a simple one, $1+\frac { 1 }{ 3 } +\frac { 1 }{ 9 } +\dots \dots =p......⓵$

Times both side by three,

$3+1+\frac { 1 }{ 3 } +\frac { 1 }{ 9 } +\dots \dots =3p ........⓶$

⓶ - ⓵: $3p - p =3$ Hence, answer is 1.5

Sum of geometric series

S_\inf=a/(1-r)

S_\inf=1/(1-1/3)

Multiply numerator and denominator by 3.

S_\inf=3/(3-1)

S_\inf=3/2=1.5