So I am back on the Surface! [Part II]
My skeletal friends, Sans and Papyrus, came over to my house today! Papyrus wanted to measure how tall I've grown, while Sans went to talk with my mother for a little while. Papyrus brought some pizza on the way as well, and he cut it in a kind of interesting way (using an enormous hexagonal cookie mold that he borrowed from my father) ...
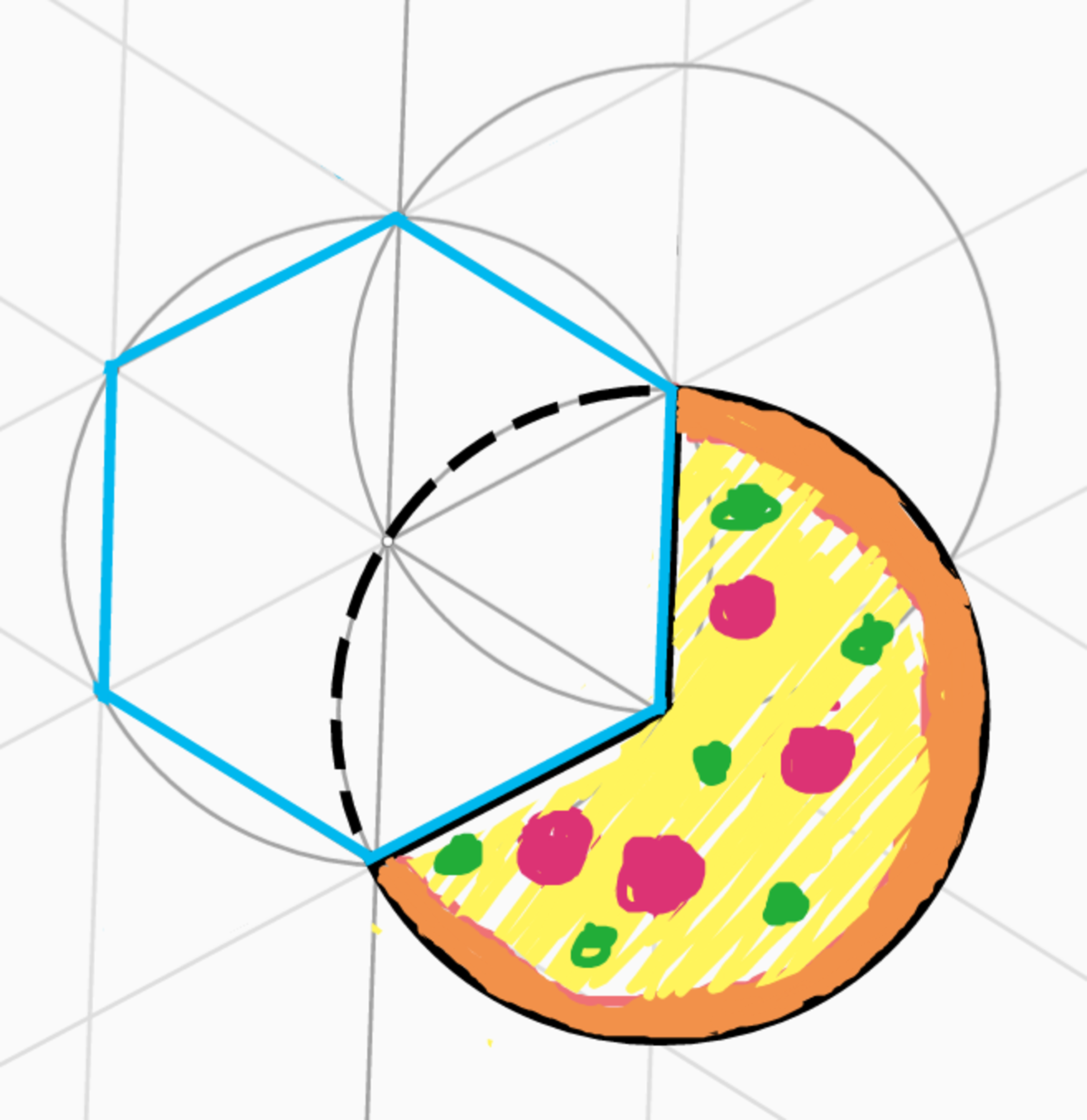
As soon as he did that, Sans posed me a challenge:
I will bet you 5 0 0 G
if you guess the perimeter of the remains of the pizza
Papyrus then told me some useful information to help...
• The hexagon he used to cut it was regular, and had a perimeter of 2 1
• He cut it from the perfect centre; he has great skill as a chef
• We should only count whole black lines from the diagram, dotted lines and blue lines are not to be counted... (which means the sum of the two radii and the arc of the sector)
Final answer should be given to two decimal places
Whoever wants to submit a report for this problem can go here
The answer is 21.66.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
A different approach @James Watson , using arc length formula :)
Given that the regular hexagon has a perimeter of 21, we find that the length of one of the sides is 6 2 1 = 2 7 . This is useful because this side length is also the radius of the circle.
Now, we can use this radius to work out the pizza's circular perimeter. Since there is only 3 2 of the pizza left, we need to find 3 2 of the total circular perimeter: 2 ( 2 7 ) π × 3 2 = 3 1 4 π
Finally, to get the full perimeter of the sliced pizza, we have to add 2 radii:
3 1 4 π + 2 ( 2 7 ) = 2 1 . 6 6
Thanks for solving my question @James Watson !
Log in to reply
lol @Frisk Dreemurr , shouldn't Papyrus give you some spaghetti instead? And an interesting way to use the camouflaged link at the bottom.
Great solution! Upvoted!
.
P e r i m e t e r c u t p i z z a = 2 r + P e r i m e t e r f u l l p i z z a − C u t A r c L e n g t h
.
P e r i m e t e r f u l l p i z z a = 2 π r = 2 × π × 3 . 5 = 2 1 . 9 9 1 1 4 8 5 7 5 1 …
.
C u t A r c L e n g t h = r θ = r a d i u s × a n g l e s u b t e n d i n g a r c = 3 . 5 × 2 . 0 9 4 4 R a d i a n s = 7 . 3 3 0 4
.
2 r + P e r i m e t e r f u l l p i z z a − C u t A r c L e n g t h = 7 + 2 1 . 9 9 1 1 4 8 5 7 5 1 − 7 . 3 3 0 4 = 2 1 . 6 6 0 7 4 … ≈ 2 1 . 6 6