So Many Intersections
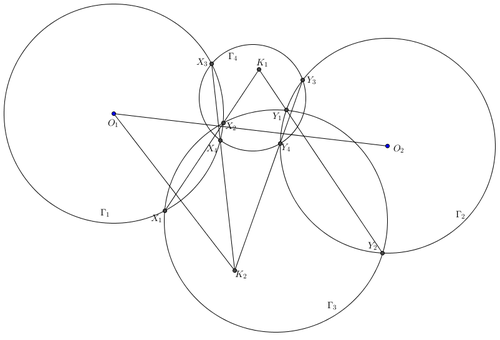Two non-intersecting circles in the plane
and
are drawn centered at points
and
respectively. A circle
intersects
at points
and
at points
Another circle
intersects
at points
and
at points
Suppose lines
and
intersect at
and
and
intersect at
Find
in degrees.
The answer is 90.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Note that X 1 X 2 is the radical axis of Γ 1 and Γ 3 and Y 1 Y 2 is the radical axis of Γ 2 and Γ 3 . Their point of intersection, K 1 , therefore is the radical center of Γ 1 , Γ 2 , Γ 3 , which implies K 1 lies on the radical axis of Γ 1 and Γ 2 . Similarly K 2 also lies on the radical axis of Γ 1 and Γ 2 . It follows that K 1 K 2 ⊥ O 1 O 2 , and ∠ K O 2 O 1 + ∠ O 2 K 1 K 2 = 1 8 0 ∘ − 9 0 ∘ = 9 0 ∘ .