So Many Triangles !
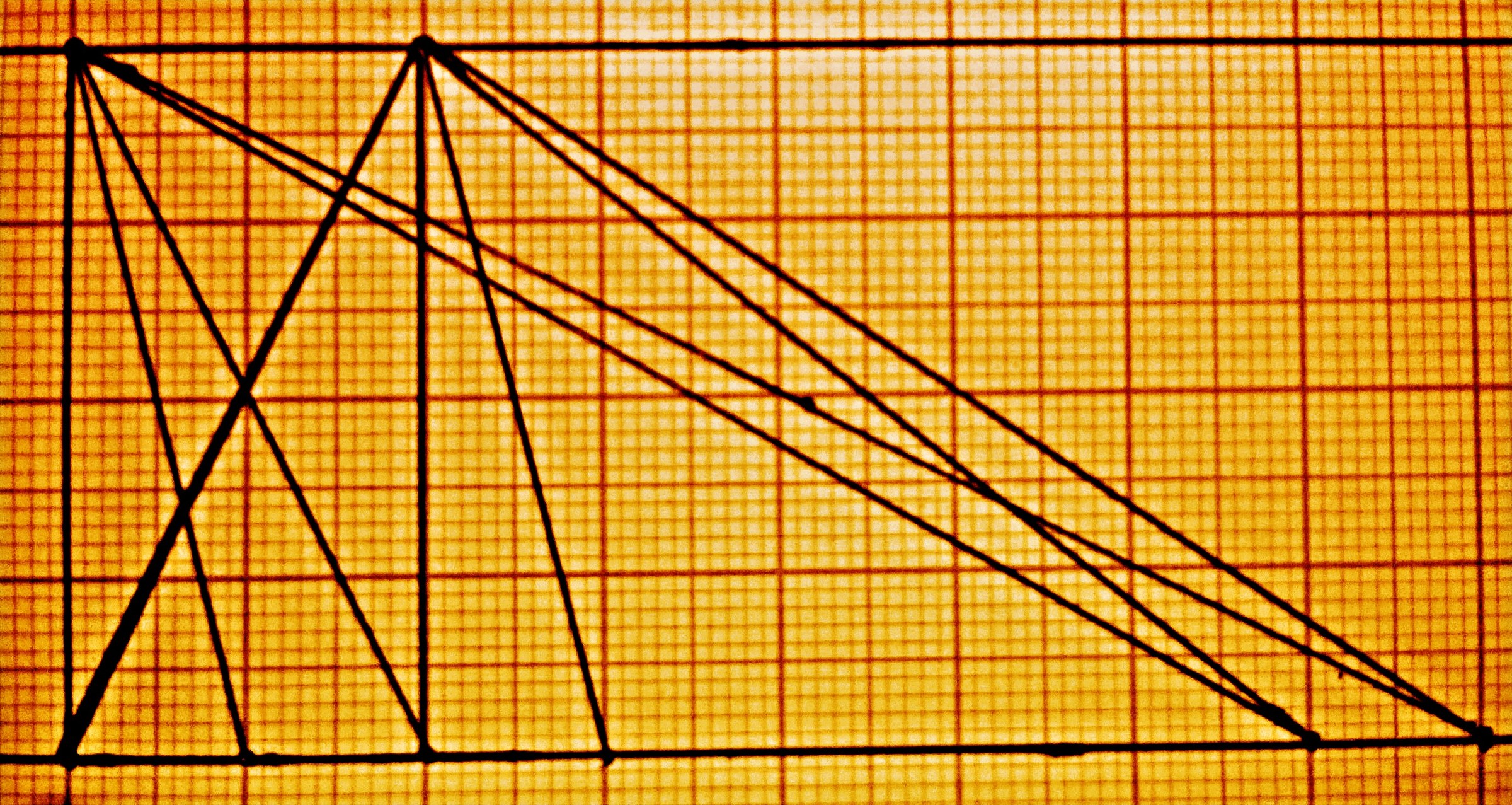Imagine a mathematical world,in which different types of geometrical shapes are living creatures.
Now look at the image above and think that triangles of different areas are belongs to different tribes.
Now,what is the population of the most populous tribe ?
Note: Consider only those triangles whose end points or vertices are on the two bold horizontal lines.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
So as the story says,different tribes are distinguished by their areas and in this scenario we are considering triangles;whose areas depends only upon the lengths of their base and height.And it's clear from the above image that all the triangles(whose vertices are only on the two horizontal bold lines)have common height,so they are different in areas as per their base lengths. So let's just follow the story. So in this case tribe of a triangle is determined fundamentally by it's baselength. After careful observation you would find out that,there are only 4 tribes of triangles i.e Tt-1,Tt-2,Tt-3Tt-7,Tt-8(Here 'Tt' denotes tribe of triangles and the number represent the base length of the triangles of the corresponding tribe. At first glance it seems that there are 5 members of Tt-1, 2 members of Tt-2, 1 member in Tt-3 and 2 members are present ineach of the rest tribes. But you might be wrong in this case.By carefully observing the picture or by naming the vertices you might discover more members of different tribes.
So to things much simpler(or to easily visualise),just turn the picture up side down.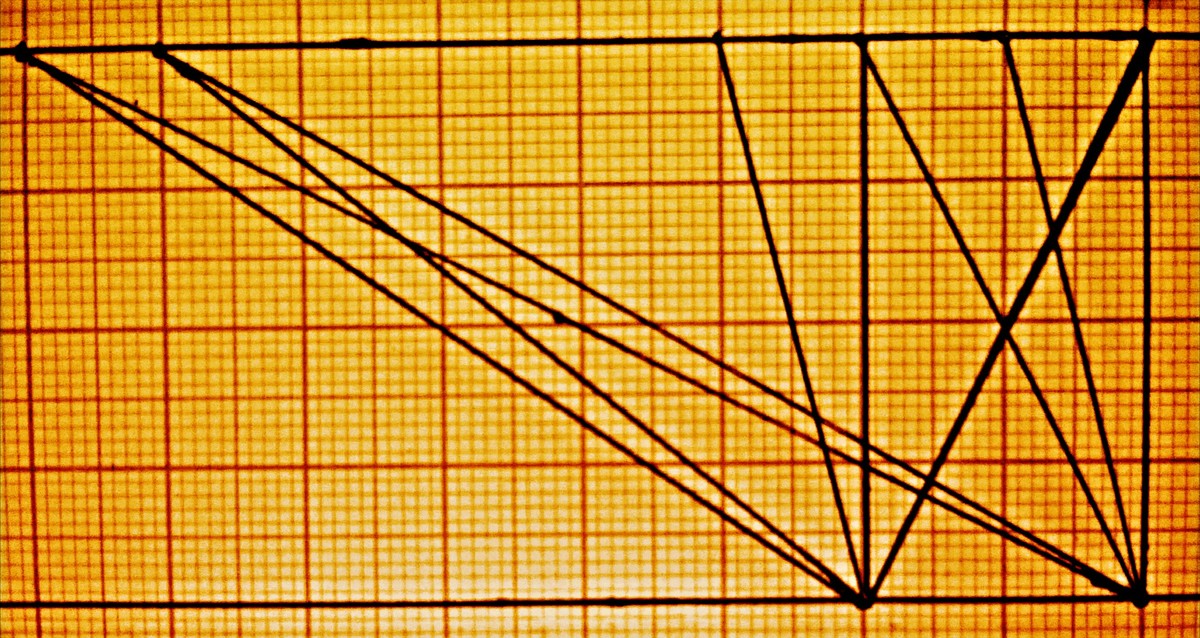
Now you can easily see 4 other members of Tt-2.So there are 6 members in Tt-2 in total i.e Tt-2 is the most populous tribe.
So the final answer is 6.