So much collisions!!

Classical Mechanics Level 3

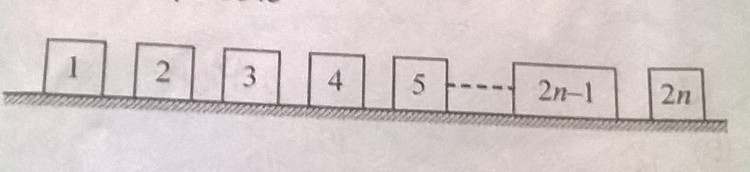2n identical cubical blocks are kept in a straight line on a horizontal smooth surface. The distance between the consecutive block is same . The block 1,3,5...(2n-1) are given velocity v to the right whereas blocks 2,4,6..,2n are given velocity to the left . All collisons between blocks are perfect elastic . The total number of collisons that will take place is?

n n+1 n(n+1) n ( n + 1 ) 2 \dfrac{n(n+1)}{2}

Prashant Kr by Prashant Kr , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

At first there will be n n collisions, after that the first and the last blocks will move away from the other blocks, then there will be n − 1 n - 1 collisions, and so on...

total number of collisions is

n + ( n − 1 ) + ( n − 2 ) + . . . + 1 = n ( n + 1 ) 2 n + (n - 1) + (n - 2) + ... + 1 = \frac{n(n+1)}{2}

4 Helpful 0 Interesting 0 Brilliant 0 Confused

That's a precise solution! So how was the Problem? To me, its brilliant, don't you argue?

Muhammad Arifur Rahman - 6 years, 1 month ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...