So restrictive
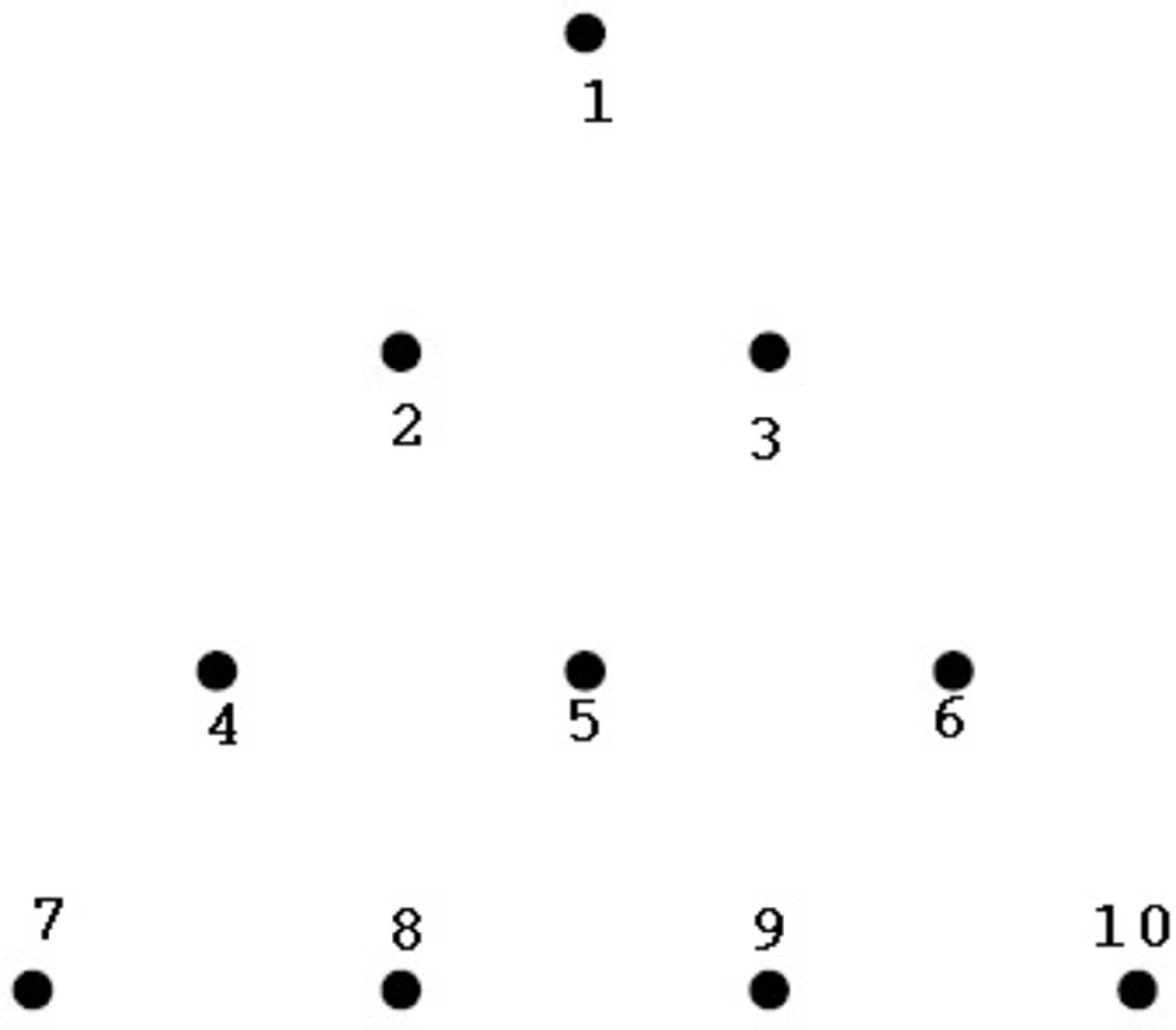
The equilateral triangular grid shown below consists of 10 points. Six of these points are to be labelled such that . How many different possible ways could the points have been labelled?
The answer is 84.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We label the vertices of the grid 1 to 10 such that the top vertex is 1, the second row is 2,3 etc. We will first determine the possible configurations up to all possible symmetry and then count the number of ways to obtain each configuration.
Notice that there are exactly 5 possible distances between pairs of points. From the vertex 1, the vertices 7 and 10 have distance 3, the vertices 4 and 6 have distance 2, and the vertices 2 and 3 have distance 1. The vertices 8 and 9 have distance 7 and the vertex 5 has distance 3 . The ordering of these from largest to smallest is 3 , 7 , 2 , 3 , 1 .
We start with the point A. Since ∣ A B ∣ has length 3, each of A and B must be corner vertices, so we may assume without loss of generality that A = 1 and B = 7 . We will later multiply by 6 since to account for this, since there are 6 ways to assign A and B to corner vertices. ∣ B C ∣ is the next longest length so either C = 3 , or C = 6 .
When C = 6 , the only choice for D is D = 4 . Then either E = 3 and there are 2 choices for F or E = 9 and there are 3 choices for F . This gives 5 possibilities for C , D , E , F .
When C = 3 then either D = 8 or 1 0 . If D = 8 , then either E = 2 and there are 2 choices for F or E = 6 and there are 2 choices for F . If D = 1 0 , then E = 5 and there are 5 choices for F . This gives 9 possibilities for C , D , E , F .
This gives a total of 5 + 9 = 1 4 choices for C , D , E , F once A , B have been fixed. There are 6 possible choices for A , B since we are choosing corner points for them. So in total, there are 1 4 × 6 = 8 4 ways the points could be labelled.