Soccer Ball problems
The surface of a soccer ball is covered with pentagons and hexagons in such a way that one pentagon and two hexagons meet at each vertex.
Now, more mathematically, let's assume that a soccer ball is a truncated icosahedron with 12 identical regular pentagons and 20 identical regular hexagons.
The fraction of the pentagonal area on the surface of the polyhedral soccer ball can be expressed as F = φ + a − b φ 2 φ , where φ = 2 1 + 5 is the golden ratio , and a , b are integers. What is a − b ?
The answer is 36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Excellent solution....
Slight mistake... Within the sqrt it will be (48-12 phi^2) not (48 - 36 phi^2)
When 2*sqrt(3) is brought within the root, then it becomes 12 not 36.
Log in to reply
Thanks. I forgot to submit the original solution. Then it was somehow lost when I go to Recent Problems. I must have redone it in a hurry.
I get so demotivated everyday, I'm never in the right track, I've got so much to learn it almost feels too much
The area of a pentagon with side s is A p = 4 1 5 ( 5 + 2 5 ) s 2 and the area of a hexagon with side s is A h = 2 3 3 s 2 . The fraction of the area of the 1 2 pentagons to the area of the 1 2 pentagons and 2 0 hexagons is then
F = 1 2 A p + 2 0 A h 1 2 A p = 1 + 1 2 A p 2 0 A h 1 = φ + 3 A p 5 φ A h φ
The term 3 A p 5 φ A h can be simplified to
3 A p 5 φ A h = 3 ⋅ 4 1 5 ( 5 + 2 5 ) s 2 5 φ ⋅ 2 3 3 s 2 = 5 ( 5 + 2 5 ) 1 0 φ 3 = 5 + 2 5 6 0 φ 2 = ( 5 + 2 5 ) ( 5 − 2 5 ) 6 0 φ 2 ( 5 − 2 5 ) = 1 2 φ 2 ( 5 − 2 5 ) = 1 2 2 1 ( 3 + 5 ) ( 5 − 2 5 ) = 6 ( 5 − 5 ) = 6 ( 8 − ( 3 + 5 ) ) = 1 2 ( 4 − 2 1 ( 3 + 5 ) ) = 4 8 − 1 2 φ 2
Therefore,
F = φ + 4 8 − 1 2 φ 2 φ
so a = 4 8 and b = 1 2 and a − b = 3 6 .
The problem is how to show that cos 36 = phi/2 without resorting to calculators, square roots of 5 or assertion of "standard" results. After that the rest is straightforward. I shall assume only that phi is the positive root of x^2 -x - 1 =0. Now consider triangle ABC, with BC = 1 and angles ABC and ACB = 72, so angle BAC = 36. Then take D on AC so that DBC = 36, and therefore ABD = 36 and BDC = 72. Thus, from isosceles triangles, ABD and BDC, AD = BD = BC = 1. Let AB = x. Then by similar triangles ABC and BDC, AB/BD = BC/DC, i.e. x/1 = 1/(x-1), so x^2 -x -1 = 0, so x = phi. (This is all standard stuff, but I don't want to be accused of assuming too much!) Now let E be the mid-point of AB, so cos 36 = AE/AD = (phi/2)/1 = phi/2
The area of a hexagon with a edge of 1 is 2 3 3 . The area of a pentagon with edge of 1 is 4 1 5 ( 2 5 + 5 ) . f = 1 + 2 1 5 − 6 5 1 . After multiplying by 1 in the form ϕ ϕ and moving the ϕ inside the square root, f = ϕ + 4 8 − 1 2 ϕ 2 ϕ results. The answer is 36.
The area of a regular polygon of n sides of unit side length is given by A n = 4 n cot n π (see Note 1). Then we have:
F = 1 2 A 5 + 2 0 A 6 1 2 A 5 = 1 5 cot 5 π + 3 0 cot 6 π 1 5 cot 5 π = cot 5 π + 2 3 cot 5 π = 1 + 2 3 tan 5 π 1 = 1 + 2 3 ⋅ φ 4 − φ 2 1 = φ + 4 8 − 1 2 φ 2 φ Divide up and down by 15 Multiply up and down by tan 5 π Note 2: cos 5 π = 2 φ ⟹ sin 5 π = 2 4 − φ 2
Therefore, a − b = 4 8 − 1 2 = 3 6 .
Notes: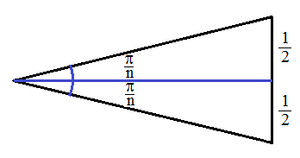
A n -side regular polygon of unit side length is made up of n congruent isosceles triangles with the unit side as base. The angle between the equal sides is n 2 π . The area of a triangle is A △ = 2 1 × tan n π 2 1 = 4 1 cot n π . The area of the n -side regular polygon A n = n A △ = 4 n cot n π .
Considering the following:
cos 5 π + cos 5 3 π cos 5 π − cos 5 2 π cos 5 π − 2 cos 2 5 π + 1 ⟹ 4 cos 2 5 π − 2 cos 5 π − 1 ⟹ cos 5 π = 2 1 = 2 1 = 2 1 = 0 = 2 1 + 5 = 2 φ Note that cos ( π − θ ) = − cos θ Note that cos 5 π > 0