Soddy Circles
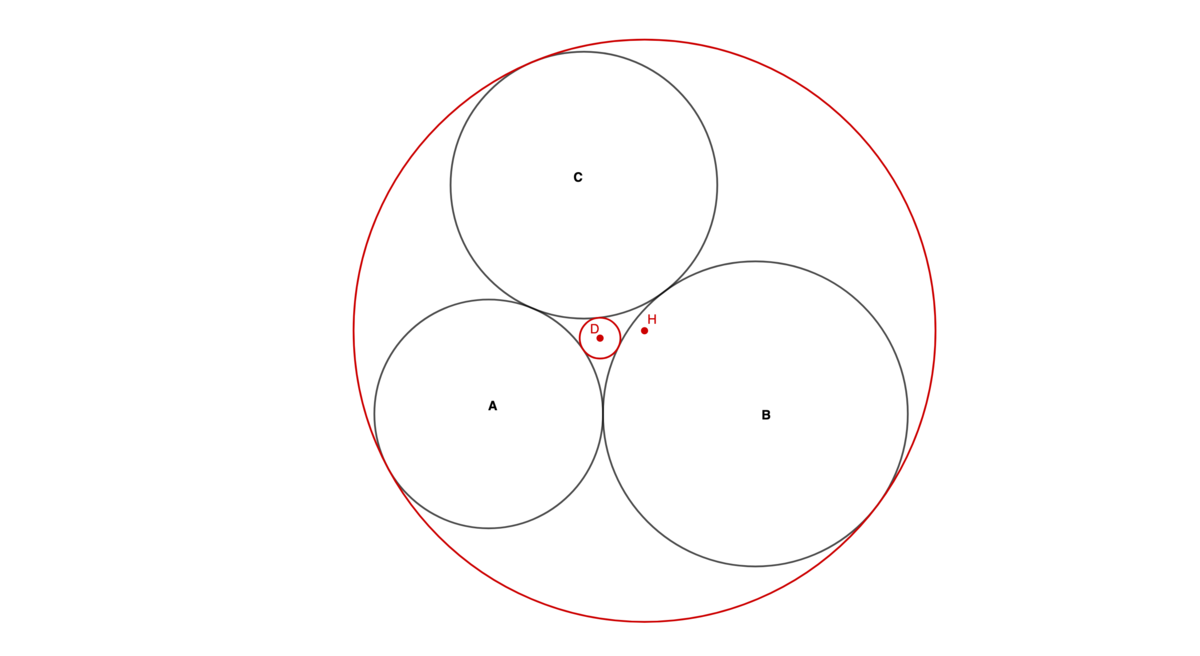
Call the black circles A , B , and C . They have radii 6 , 8 , and 7 respectively, and are mutually tangent. The small red circle with center D is externally tangent to the three black circles. The large red circle with center H is internally tangent to the black circles. Find the distance D H . If D H is expressed as c a b submit a + b + c .
Brilliant has a nice wiki page on these types of problems.
The answer is 2436.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thank you for the solution, Mark. I had studied Dergiades’ paper while designing this problem, but I was unfamiliar with barycentric coordinates, so had a bit of a learning curve. It was worth the effort!
-
Find radius for two Soddy circles - 1 5 7 1 6 8 , 1 1 1 6 8 .
-
If A ( 0 , 0 ) and C ( 1 3 , 0 ) - centers of circles. Find points H and D - SoddyCircles Centers.
-
D H = ( 2 0 4 1 1 2 0 7 8 − 1 4 3 1 0 2 6 ) 2 + ( 2 0 4 1 7 8 9 6 − 1 4 3 8 4 0 ) 2 = 1 7 2 7 6 7 2 3 7
Answer 2 4 3 6 .
Nice use of Alpha. Very clear. Did you mean to say C ( 0 , 1 3 ) instread of C ( 1 3 , 0 ) ? Your equations are set up that way.
If the lengths of the sides of A B C are a , b , c as usual, then the nonnormalised barycentric coordinates of the centres D , H of the two Soddy circles are D ^ = ( a + s − a Δ , b + s − b Δ , c + s − c Δ ) H ^ = ( a − s − a Δ , b − s − b Δ , c − s − c Δ ) respectively, where s = 2 1 ( a + b + c ) is the semiperimeter and Δ = s ( s − a ) ( s − b ) ( s − c ) is the area of A B C .
If we normalise the barycentric coordinates of each point, so that the coefficients sum to 1 , obtaining P = u + v + w 1 ( u , v , w ) w h e r e D ^ = ( u , v , w ) and similarly obtaining Q from H ^ , and if we calculate P − Q = ( x , y , z ) , then the distance D H between the two Soddy circles is given by the formula D H 2 = − a 2 y z − b 2 x z − c 2 x y In this case we have a = 6 + 7 = 1 3 , b = 6 + 8 = 1 4 , c = 7 + 8 = 1 5 , so that s = 2 1 , Δ = 8 4 and hence D H = 1 7 2 7 6 7 2 3 7 making the answer 6 7 2 + 3 7 + 1 7 2 7 = 2 4 3 6 .