Soldier Lines Riddle
Two troops, each with a perfect square number of soldiers, were marching in lines. Upon meeting the other troop, one group would stand fixed on their positions while the other group of soldiers would get in lines with the same numbers of soldiers in each row as much as possible.
As an explicit example below, if there were soldiers in one troop and in the other, there would be ways of merging the lines. As shown, there would be a remainder of soldier (marked with red) in either formation.
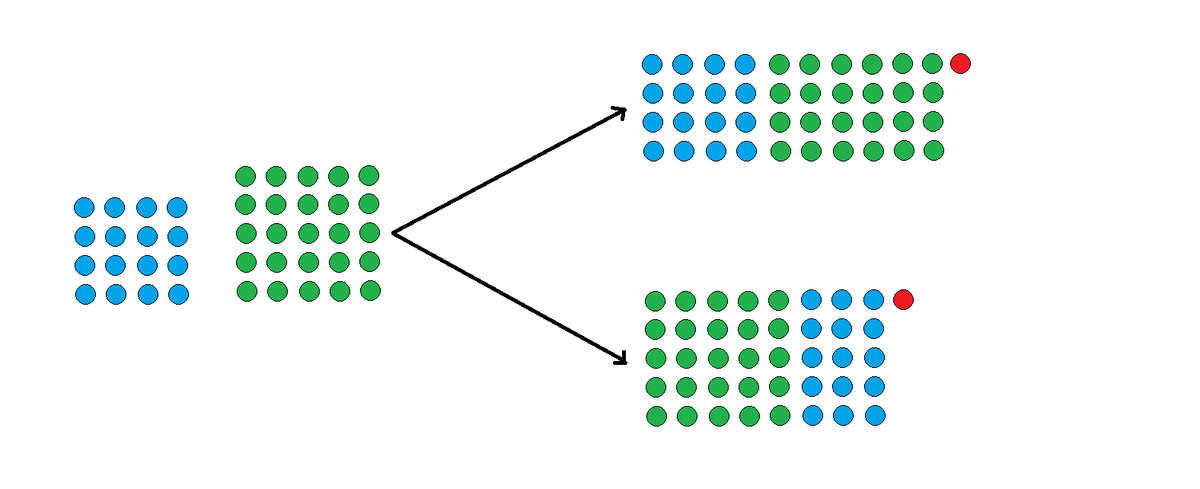
After joining together, if there were a remainder of soldiers in one formation and remainder of in the other, what would be the least possible total number of soldiers?
The answer is 410.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let x be the number of lines in one group and y be that in the other for integers y > 2 and x > 3 . We could set up the system of equilavences as show below:
x 2 ≡ 2 ( m o d y ) y 2 ≡ 3 ( m o d x )
Then let d = ∣ x − y ∣ . We can then substitute d 2 into the equivalences with d 2 > 3 or d > 1 :
x 2 ≡ ( x − y ) 2 ≡ d 2 ≡ 2 ( m o d y ) y 2 ≡ ( y − x ) 2 ≡ d 2 ≡ 3 ( m o d x )
Now we will rewrite the system as equations for some integer quotients n , m :
d 2 = n y + 2 d 2 = m x + 3
Thus, n y − m x = 1 , and according to Bezout's identity, gcd(x,y) = 1, and gcd(m,n) = 1.
Solving for x , y , we will get:
y = n d 2 − 2 x = m d 2 − 3
That means d = ∣ x − y ∣ = ∣ m d 2 − 3 − n d 2 − 2 ∣ . Then d m n = ∣ ( m − n ) d 2 − 2 m + 3 n ∣ = ∣ ( m − n ) ( d 2 − 2 ) + n ∣ = ∣ ( m − n ) ( n y ) + n ∣ . Dividing by n both sides, d m = ∣ ( m − n ) y + 1 ∣ . Thus, d m ≡ ∣ 1 ∣ ≡ 1 ( m o d y ) for y > x .
Let us check cases, where y > x and that y = x + d .
From the above equation, we could also set up d m ≡ 1 ( m o d m − n ) . Since m − n ≡ 0 ( m o d m − n ) , then m ≡ n ( m o d m − n ) . Thus, d is a modular inverse of m and n . Then d n ≡ 1 ( m o d m − n ) , and ( d 2 − 2 ) n ≡ d − 2 n ( m o d m − n ) .
Substituting n y = d 2 − 2 , we will get n 2 y ≡ d − 2 n ( m o d m − n ) .
n 2 y − 2 n ≡ d ( m o d m − n ) .
( n y ) 2 − 2 n y ≡ d y ( m o d y ( m − n ) ) .
( m x + 1 ) 2 − 2 ( m x + 1 ) ≡ d y ( m o d y ( m − n ) ) .
( m x ) 2 − 1 ≡ d y ( m o d y ( m − n ) ) .
( m x − 1 ) ( m x + 1 ) ≡ d y ( m o d y ( m − n ) ) .
( m x − 1 ) ( n y ) ≡ d y ( m o d y ( m − n ) ) .
( m x − 1 ) ( n ) ≡ d ( m o d ( m − n ) ) .
m x − 1 ≡ d 2 ( m o d ( m − n ) ) .
m x + 3 ≡ d 2 + 4 ( m o d ( m − n ) ) .
d 2 ≡ d 2 + 4 ( m o d ( m − n ) ) .
Finally, 4 ≡ 0 ( m o d m − n ) . That means m − n ∣ 4 , and the value of m − n is either 1 , 2 , or 4 .
However, by checking values of d = 2 , 3 , 4 , no answers can be found:
For d = 2 , d 2 = 4 ≡ 3 ( m o d x ) ; 1 ≡ 0 ( m o d x ) , which is contradicted because x > 3 .
For d = 3 , d 2 = 9 ≡ 2 ( m o d y ) ; 7 ≡ 0 ( m o d y ) . Only y = 7 works, leading to x = 7 − 3 = 4 , but d 2 − 3 = 9 − 3 = 6 , which is not divisible by 4 and so contradicted.
For d = 4 , d 2 = 1 6 ≡ 2 ( m o d y ) ; 1 4 ≡ 0 ( m o d y ) . Again, only y = 7 works, leading to x = 7 − 4 = 3 , but d 2 − 3 = 1 6 − 3 = 1 3 , which is not divisible by 3 and so contradicted.
By all means, we can conclude that d > m − n . Returning to d m = ( m − n ) y + 1 . d ( m − d 1 ) = ( m − n ) y . Since d > m − n , then y > m − d 1 . With both y , m being integers, we can conclude y > m .
Returning to d m ≡ 1 ( m o d y ) . d 2 m ≡ d ( m o d y ) . Since d 2 = n y + 2 , then d 2 ≡ 2 ( m o d y ) . Thus, 2 m ≡ d ( m o d y ) , and m = d − m ( m o d y ) . We know that y > m and y > d , so that means y > ∣ d − m ∣ . Here are the 3 possible scenarios:
First, d − m = 0 , that makes m = 0 ( m o d y ) , which is contradicted because y > m .
Second, d − m < 0 , with y > m and y > d , the resulting 2 m − d ≡ 0 ( m o d y ) only applies for y = 2 m − d . For any higher quotient before y will make an inequality. Then x + d = 2 m − d , and so x = m d 2 − 3 = 2 ( m − d ) . Rearranging the quadratic equation, we will obtain d 2 + ( 2 m ) d − ( 2 m 2 + 3 ) = 0 . By the quadratic formula, d = − m + 3 ( m 2 + 1 ) . In order to yield integer d , m 2 + 1 = 3 t 2 for some integer t . However, per modulo 3 , m 2 ≡ − 1 ( m o d 3 ) , and for all perfect squares modulo 3 , it only results in a remainder of 1 or 0 only. Thus, this is contradicted.
As a result, y > d − m > 0 and y > m . Thus, in order for the remainders m ≡ d − m ( m o d y ) to be true, it needs to be m = d − m . Thus, d = 2 m . Then d 2 = 4 m 2 = m x + 3 , and so m ( 4 m − x ) = 3 . That means m ∣ 3 , leaving only m = 1 or m = 3 , but for m = 1 , it will cause d = 2 , which is shown to be contradicted earlier.
Since no lesser d is applicable, the other cases, where x > y wouldn't result in least possible solution.
Finally, m = 3 ; d = 6 , and 3 6 ≡ 2 ( m o d y ) . 3 4 = 2 × 1 7 ≡ 0 ( m o d y ) . Clearly, n = 2 and y = 1 7 , and x = 1 7 − 6 = 1 1 .
Therefore, the total number of soldiers = 1 1 2 + 1 7 2 = 4 1 0 .
Checking the answers, we can prove the solution:
1 1 2 = 1 7 × 7 + 2
1 7 2 = 1 1 × 2 6 + 3