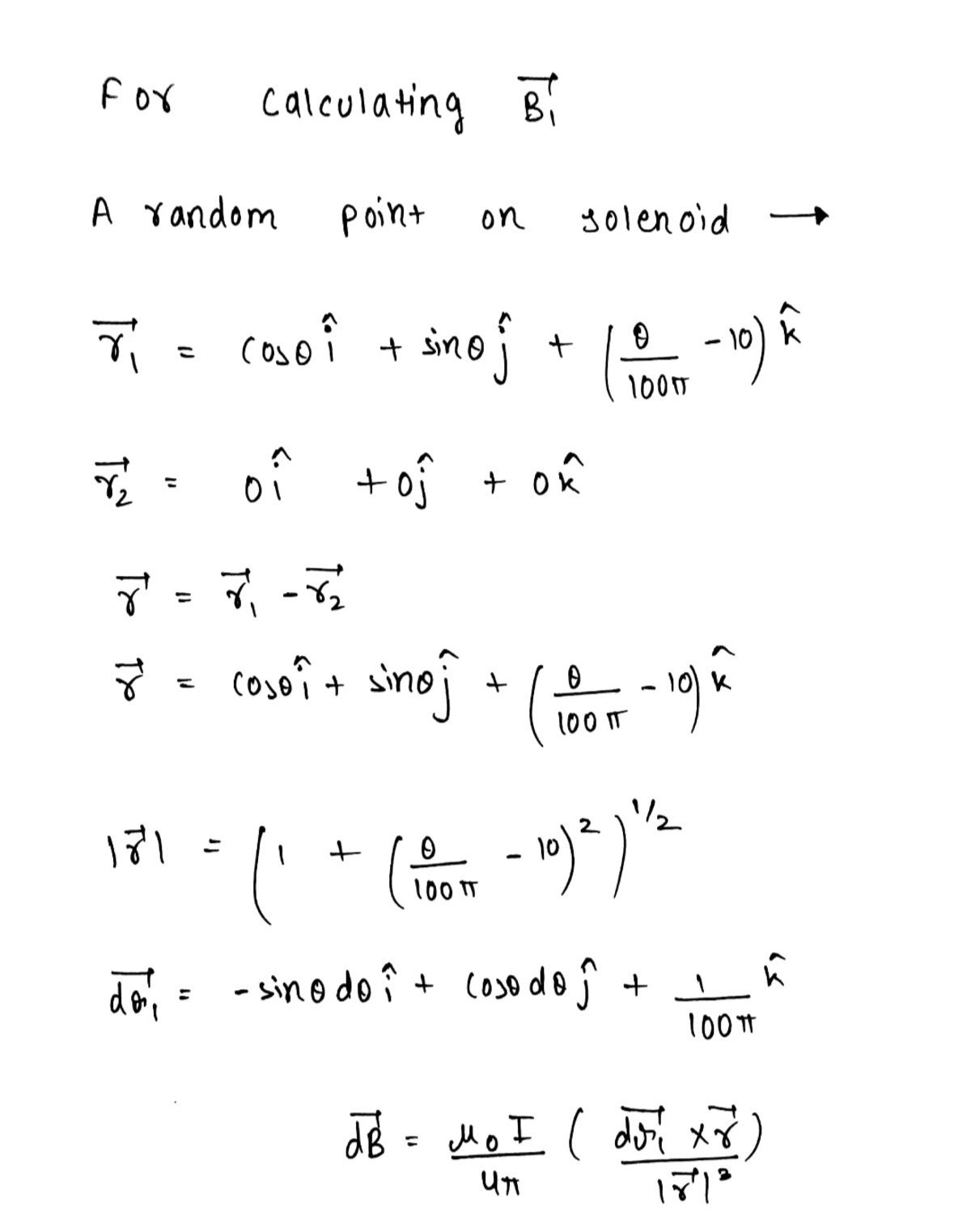Solenoid Exercise
A wire solenoid has the following shape:
x = cos θ y = sin θ z = − 1 0 + 1 0 0 π θ 0 ≤ θ ≤ 2 0 0 0 π
The solenoid carries 1 unit of electric current. Let B 1 be the magnitude of the magnetic flux density at point ( x 1 , y 1 , z 1 ) = ( 0 , 0 , 0 ) , and let B 2 be the magnitude of the magnetic flux density at point ( x 2 , y 2 , z 2 ) = ( 2 , 0 , 0 ) .
What is B 2 B 1 ?
Details and Assumptions:
1)
Magnetic permeability
μ
0
=
1
2)
Only the fields from the solenoid are to be counted (don't worry about completing the circuit, etc.)
Note: How does the value of B 1 compare to the value given by the standard formula for a solenoid magnetic field?
The answer is 201.15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Consider a point on the solenoid as such:
r p = cos θ i ^ + sin θ j ^ + ( − 1 0 + 1 0 0 π θ ) k ^
An arc length element tangential to the point is:
d r p = ( − sin θ i ^ + cos θ j ^ + ( 1 0 0 π 1 ) k ^ ) d θ
Consider the point of interest at which field is to be computed to be:
r c 1 = 0 i ^ + 0 j ^ + 0 k ^ r c 2 = 2 i ^ + 0 j ^ + 0 k ^
In general, the point of interest will be denoted by r c . The vector joining a point on the solenoid and the point of interest, and directed towards the point of interest, is:
r = r c − r p
Now, Biot-Savart Law is applied:
d B = 4 π μ o I ( ∣ r ∣ 3 d r p × r ) = f x ( θ ) i ^ + f y ( θ ) j ^ + f z ( θ ) k ^
d B has three components each of which is a function of θ only. This gives three integrals:
B
x
=
∫
0
2
0
0
0
π
f
x
(
θ
)
d
θ
B
y
=
∫
0
2
0
0
0
π
f
y
(
θ
)
d
θ
B
z
=
∫
0
2
0
0
0
π
f
z
(
θ
)
d
θ
I have written a script of code to compute the answer for each case which turns out to be:
B 2 B 1 ≈ 2 0 1 . 1 5 2 8
As for the bonus question, In the first case, the field magnitude turns out to be:
B 1 ≈ 4 9 . 7 5
Which is almost close to the result produced by the standard formula which turns out to be 5 0 . This is unlike the case where
B 2 ≈ 0 . 2 4 7 3
This result highly deviates from the standard formula prediction. It is surprising that just an offset of two units in the point of interest can produce such a different result. In my opinion, the standard formula holds true provided the test point is sufficiently and equally far from either end of the solenoid. I am yet to test this speculation, however.
@Karan Chatrath can you please post the analytical solution of Starfish orbit .
As sir @Karan Chatrath has provided a very nice solution. I will just elaborate the solution. This problem can be considered as a biot-savart law problem because we have the exact information of solenoid structure.