Solid angle subtended by a segmented circle by HCR

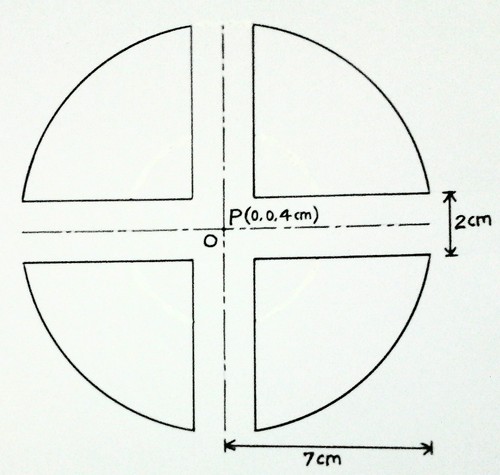The diagram above shows a segmented circular plane, centered at the origin 'O', having a radius 7 cm. Two identical rectangular strips, each having width 2 cm, are thoroughly cut off & removed from the circular plane along x & y axes. Thus four identical segments of the circular plane are left over. Calculate the solid angle (in Ste-radian) subtended by the remaining plane (consisting of four identical segments) at a point P (0, 0, 4 cm) lying on the z-axis (normally outwards to the plane of paper).

Hint: Solid angle subtended by a circular plane, with a radius r, at any point lying on the vertical axis at a distance d from the center, is given as

$\large \Omega=2\pi \left(1-\frac{d}{\sqrt{d^2+r^2}} \right)$