Solution Attempt for Two Grounded Spheres
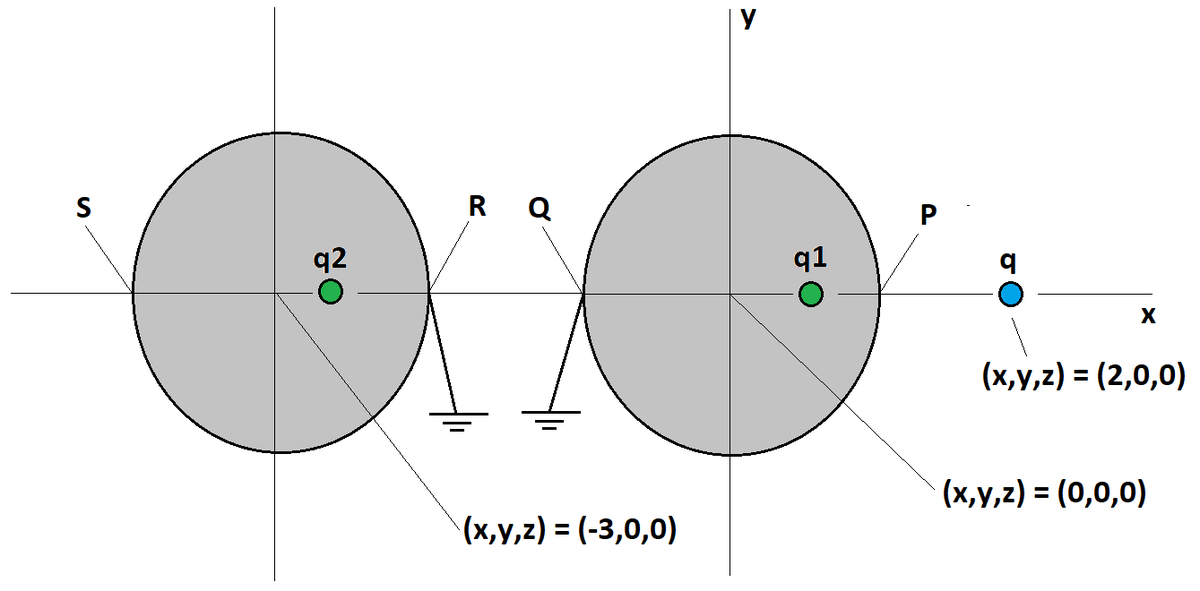
Two grounded conducting spheres of radius 1 have their centers at different places on the x axis, as shown in the diagram. A positive charge q is positioned on the x axis outside both of the spheres. Suppose we try to extend the image-charge solution method to this case. Find two virtual image charges q 1 and q 2 , positioned on the x axis within their respective spheres, such that the electric potential is zero at points P , Q , R , and S . What is the value of q 2 ?
Unfortunately, this charge distribution does not result in zero potential over the entirety of both sphere surfaces. It is thus not a proper electrostatic solution. I wonder what the true charge distribution is.
Details and Assumptions:
1)
q
=
+
1
2)
4
π
ϵ
0
1
=
1
3)
Be mindful of the signs of the charges
The answer is -0.06707.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let the coordinates of q 1 be ( x 1 , 0 ) and that of q 2 be ( x 2 , 0 ) .
Then the potentials evaluated at points P , Q , R and S are:
V P = 1 + 1 − x 2 q 2 + 1 − x 1 q 1 = 0 V Q = x 1 + 1 q 1 − x 2 + 1 q 2 + 3 1 = 0 V R = x 1 + 2 q 1 − x 2 + 2 q 2 + 4 1 = 0 V S = x 1 + 4 q 1 + x 2 + 4 q 2 + 6 1 = 0
These potentials are calculated by assuming that q 1 is between P and Q and q 2 is between R and S .
There are four equations with four unknowns and the equations are nonlinear. Solving using an approach like Newton-Raphson gives the answer of
q 2 = − 0 . 0 6 7 0 7
Of course, the starting point is crucial for the Newton-Raphson method to converge. I chose one where x 1 o = 0 . 5 and x 2 o = − 2 . 5 .
If the potentials are calculated by not by assuming that q 1 is between P and Q and q 2 is between R and S , and by arbitrarily placing them anywhere along the positive X-axis, the potential equations are:
V P = x 1 − 1 q 1 + x 2 − 1 q 2 + 1 = 0 V Q = x 1 + 1 q 1 + x 2 + 1 q 2 + 3 1 = 0 V R = x 1 + 2 q 1 + x 2 + 2 q 2 + 4 1 = 0 V S = x 1 + 4 q 1 + x 2 + 4 q 2 + 6 1 = 0
In this case, the numerical equation solver spits out singularities. In principle, either set of equations should yield the answer, but it is not the case here. I wonder why.
Hope I am able to explain my difficulty.
As for the image-charge solution method, I have not fully understood the article yet. I am just treating these as simple electrostatics problems without dwelling much on the interpretation of the results and charge distributions, for now,
I used a hill-climbing algorithm to solve. My initial program used sensible initial conditions, like yours. When I make my initial conditions more random, the program chooses a very silly solution.
x 1 = 2 q 1 = − 1 x 2 = don’t care q 2 = 0
This solution works, but it is ridiculous. And there are infinitely many possible positions for x 2 , given that q 2 = 0 . So that may be where your singularities are coming from. There are, in fact, infinitely many possible junk solutions.
Log in to reply
Okay, the solution you showed was in fact one of the ones I obtained. Thanks for the clarification.
You obviously need to restrict the solution space to 0 < x 1 < 1 and − 3 < x 2 < − 2 . Anything else is unreasonable. With these constraints, the solution is unique. Obviously, the junk solution above is where there is no external charge, so everywhere is a zero potential!
def f(r1,r2):
try:
q2=(1/(r1+4)
(1/4)-(1/6)
1/(r1+2))/(1/(r1+2)
1/(1+r2)-1/(1-r2)
1/(r1+4))
q1=(1/6
1/(1-r2)-1/4
1/(1+r2))/(1/(r1+2)
1/(1+r2)-1/(1-r2)
1/(r1+4))
if abs(q2/(2-r2)+q1/(1+r1)+1/3)<=0.0002 and abs(q1/(1-r1)+q2/(4-r2)+1)<=0.0002:
print (q2)
except ZeroDivisionError:
1
r1,r2=0,0
while(r1<1):
r2=0
while(r2<1):
f(r1,r2)
r2+=0.001
r1+=0.001
The main problem was solved by Karan's method.
As to the general problem, we first create an image charge of q 1 = − 2 1 q at the point ( 2 1 , 0 , 0 ) . This gives a zero potential on the right-hand sphere. Then add charges q 2 , q 3 inside the LH sphere to be inverse charges to q , q 1 with respect to the LH sphere. This gives the LH sphere zero potential, while spoiling the potential on the RH sphere. So we add charges q 4 , q 5 inside the RH sphere to be inverse charges to q 2 , q 3 with respect to the RH sphere to restore the zero potential on the RH sphere. Keep on going...
We end up with an infinite sequence of image charges inside each sphere. However, all the image charges are within 2 1 of the centres of their respective spheres, so no charge (except q ) introduces a singularity outside the spheres. Also the magnitudes of the charges form a sequence which converges to 0 at least exponentially. If we add up the potentials due to q , q 1 , q 2 , . . . , q 2 n − 1 we have a zero potential on one of the spheres and a nonzero potential on the other sphere which is exponentially small as a function of n . Thus we can sum the potentials due the charge q and all the images charges q n ( n ∈ N ), and we obtain a potential which is harmonic outside both spheres (except at the charge q ), zero on both spheres, with a suitable singularity at the charge q .
The mathematical details are messy, but this seems to be a way through the problem.