Solution matters more than the answer!
a 2 − a + 1 ( 2 a − 1 ) 2 + b 2 − b + 1 ( 2 b − 1 ) 2 + c 2 − c + 1 ( 2 c − 1 ) 2 + d 2 − d + 1 ( 2 d − 1 ) 2
Given nonnegative real numbers a , b , c , d which satisfy a + b + c + d = 4 , find the maximum value of the expression above to 1 decimal place.
The answer is 8.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
To understand why this is the called the "tangent line trick", consider the following graphs :
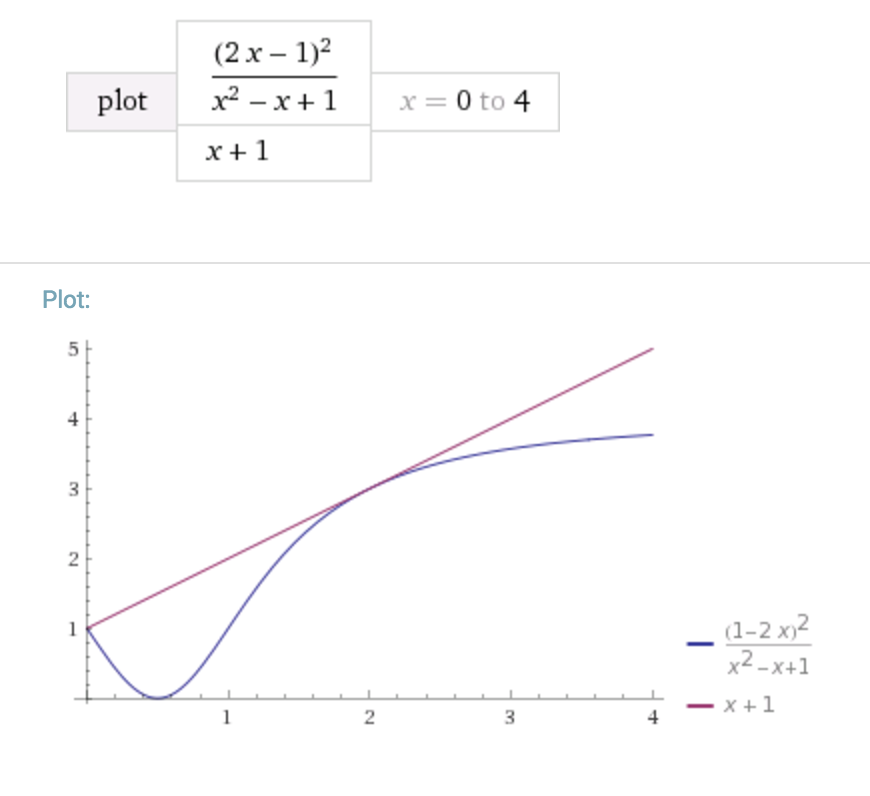
After how many trials one can get the idea of that trick ..... I mean in exams we do not have so much time
Solution: Notice that a + 1 ≥ a 2 − a + 1 ( 2 a − 1 ) 2 ⟺ a 3 + 1 ≥ 4 a 2 − 4 a + 1 ⟺ a 3 − 4 a 2 + 4 a ≥ 0 ⟺ a ( a − 2 ) 2 ≥ 0 , which is true.
Thus, a 2 − a + 1 ( 2 a − 1 ) 2 + b 2 − b + 1 ( 2 b − 1 ) 2 + c 2 − c + 1 ( 2 c − 1 ) 2 + d 2 − d + 1 ( 2 d − 1 ) 2 ≤ ( a + 1 ) + ( b + 1 ) + ( c + 1 ) + ( d + 1 ) = 8 .
Wait, where did that first inequality come from???
The answer to this question is a trick called the "tangent line trick". The tangent line trick is a trick which doesn't work so well in finding the maximum/minimum values of expressions, but it does great when it comes to proving inequalities.
The first step is to randomly guess the possible tuple ( a , b , c , d ) which yields the maximum value. A little bit of experimentation should yield the maximum to be 8 , after trying out cases when a = b = c = d , a = 0 , a = b = 0 and a = 4 .
Now that we've gotten the maximum ( 8 ) and the equality case ( a = b = 2 , c = d = 0 ) , we just need to prove this is the maximum. Here, we use the trick.
Notice that our inequality is of the form f ( a ) + f ( b ) + f ( c ) + f ( d ) ≤ 8 with a + b + c + d = 4 and f ( x ) = x 2 − x + 1 ( 2 x − 1 ) 2 . The trick here is to take the line tangent to f ( x ) at the equality case (when x = 2 ) and prove that this line is greater than or equal to f ( x ) .
(Note that this works precisely because our constraint is of the form a + b + c + d = k , and if we add up linear equations, we're bound to get the expression a + b + c + d somewhere in the sum, allowing us to use our constraint.)
Now, note that the tangent line to f ( x ) at x = a has the form f ( a ) + f ′ ( a ) ( x − a ) . A little differentiation shows us that f ′ ( 2 ) = 1 and we have that f ( 2 ) = 3 , giving us the tangent line to f ( x ) at x = 2 to be 3 + 1 ( x − 2 ) = x + 1 . Thus, our possible inequality becomes
x + 1 ≥ x 2 − x + 1 ( 2 x − 1 ) 2
Which we proved above with equality holding when x = 0 or x = 2 . Now, we proceed as we did above.