Solution of a trigonometric system of equations in two unknowns

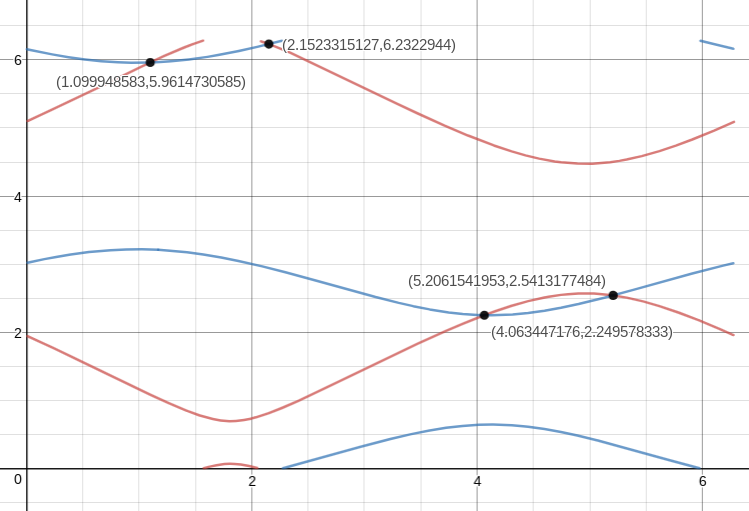
The equations can be written $\begin{aligned} 11\sin x & = \; 9\cos y - 4\sin y \\ 11\cos x & = \; 11 - 19\cos y - 38 \sin y \end{aligned}$ and hence we have the equation $121 \; = \; (9\cos y - 4\sin y)^2 + (11 - 19\cos y - 38 \sin y)^2$ which has $4$ solutions in $(0,2\pi)$ , namely $y = 2.24958\,,\,2.54132\,,\,5.96147\,,\,6.23229$ . Each value of $y$ defines the values of $\cos x$ and $\sin x$ precisely, and hence gives a unique value for $x$ in $(0,2\pi)$ . These values are $x = 4.06345\,,\,5.20615\,,\,1.09995\,,\,2.15233$ respectively. Adding up the four values for $y$ and the four values for $x$ gives the answer $\boxed{29.5065}$ .